|
旧电脑找到一个word文档(不知道原作者) 题 六边形 ABCDEF 三组对边互相平行, G, H, I, J, K, L 分别为六边中点,求证:GJ, HK, IL 三线共点。
证 连接 AD, BE, CF 。下面分两种情况讨论:
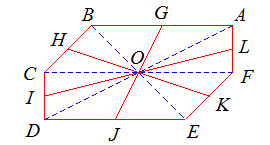
(1)AD, BE, CF 交于一点 O(见上图)。
这时有
ΔAOB~ΔDOE ,ΔBOC~ΔEOF ,ΔDOC~ΔFOA 。
$\frac{\text{AB}}{\text{DE}} = \frac{\text{OB}}{\text{OE}} = \frac{\text{BC}}{\text{EF}} = \frac{\text{OC}}{\text{OF}} = \frac{\text{CD}}{\text{FA}} = \frac{\text{OD}}{\text{OA}} = \frac{\text{DE}}{\text{AB}} = \frac{\text{OE}}{\text{OB}} = \frac{\text{EF}}{\text{BC}} = \frac{\text{OF}}{\text{OC}} = \frac{\text{FA}}{\text{CD}} = \frac{\text{OA}}{\text{OD}}$ ,
所以 AB = DE ,BC = EF ,CD = FA 。
可见 ABDE,BCEF,CDFA 都是以 O 为中心的平行四边形。
因为平行四边形对边中点连线必定通过平行四边形中心,所以 GJ, HK, IL 都通过 O 点,也就是说,GJ, HK, IL 三线共点。
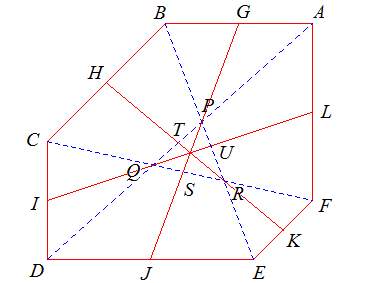
(2)AD, BE, CF不交于一点,而是分别交于 P, Q, R 三点(见上图)。
由梯形性质可知,P 点在 GJ 上,Q 点在 IL 上,R 点在 HK 上。
设 GJ 与 QR 交于 S ,HK 与 PQ 交于 T ,IL 与 RP 交于 U 。
因为 DJ = JE ,所以 $1 = \frac{S_{\Delta\text{PDJ}}}{S_{\Delta\text{PJE}}} = \frac{\frac{1}{2}\text{PD} \times \text{PJ} \times \sin\angle\text{DPJ}}{\frac{1}{2}\text{PE} \times \text{PJ} \times \sin\angle\text{EPJ}} = \frac{\text{PD} \times \sin\angle\text{DPJ}}{\text{PE} \times \sin\angle\text{EPJ}}$ 。
同理,因为 AG = GB ,所以 $1 = \frac{S_{\Delta\text{AGP}}}{S_{\Delta\text{GBP}}} = \frac{\text{AP} \times \sin\angle\text{APG}}{\text{BP} \times \sin\angle\text{BPG}} = \frac{\text{AP} \times \sin\angle\text{DPJ}}{\text{BP} \times \sin\angle\text{EPJ}}$ 。
所以 $\frac{\sin\angle\text{DPJ}}{\sin\angle\text{EPJ}} = \frac{\text{BP}}{\text{AP}} = \frac{\text{PE}}{\text{PD}} = \frac{BP + PE}{AP + PD} = \frac{\text{BE}}{\text{AD}}$ 。
在 ΔPQS 和 ΔPSR 中,由正弦定理可知,有
$QS = PQ\frac{\sin\angle\text{QPS}}{\sin\angle\text{QSP}}$ ,$SR = PQ\frac{\sin\angle\text{RPS}}{\sin\angle\text{PSR}}$ 。
所以有
$\frac{\text{QS}}{\text{SR}} = \frac{\text{PQ}\frac{\sin\angle\text{QPS}}{\sin\angle\text{QSP}}}{\text{PR}\frac{\sin\angle\text{RPS}}{\sin\angle\text{PSR}}} = \frac{\text{PQ} \times \sin\angle\text{QPS}}{\text{RP} \times \sin\angle\text{RPS}} = \frac{\text{PQ}}{\text{RP}} \times \frac{\sin\angle\text{DPJ}}{\sin\angle\text{EPJ}} = \frac{\text{PQ}}{\text{RP}} \times \frac{\text{BE}}{\text{AD}}$ 。
同理有
$\frac{\text{PT}}{\text{TQ}} = \frac{\text{RP}}{\text{QR}} \times \frac{\text{CF}}{\text{BE}}$ ,$\frac{\text{RU}}{\text{UP}} = \frac{\text{QR}}{\text{PQ}} \times \frac{\text{AD}}{\text{CF}}$ 。
可见必有
$\frac{\text{QS}}{\text{SR}} \times \frac{\text{PT}}{\text{TQ}} \times \frac{\text{RU}}{\text{UP}} = \frac{\text{PQ}}{\text{RP}} \times \frac{\text{BE}}{\text{AD}} \times \frac{\text{RP}}{\text{QR}} \times \frac{\text{CF}}{\text{BE}} \times \frac{\text{QR}}{\text{PQ}} \times \frac{\text{AD}}{\text{CF}} = 1$ 。
所以由 Ceva(塞瓦)定理的逆定理Menelaus(梅内劳斯)定理可知 PS, RT, QU 三线共点,即 GJ, HK, IL 三线共点。 |