求点A的轨迹,使△ABC满足$a = \frac{b^{2} + c^{2}}{b + c}$

hbghlyj

给定两个点B,C,求点A的轨迹,使△ABC满足$a = \frac{b^{2} + c^{2}}{b + c}$

解:设BC=a,0<b⩽c,c满足方程x² − ax − b(a−b) = 0,这表明以下结构:

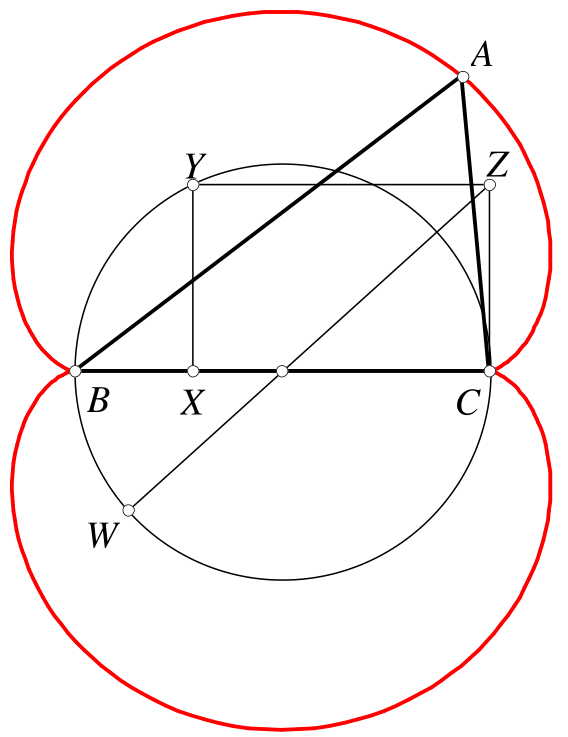
Y是以BC为直径的圆上一点,X,Z是Y在BC和过C的BC垂线上的投影,W是过Z的直径的端点,A是圆(B,WZ)与圆(C,CX)的交点.

设$B\left( - \frac{a}{2},0 \right),C\left( \frac{a}{2},0 \right)$,则A的轨迹方程为256y⁸ + 1024x²y⁶ − 96(a⁴−16x⁴)y⁴ − 32(a²−2x²)(a²+4x²)²y² − (a²−4x²)³(3a²+4x²) = 0.极坐标方程为

$$\cos{2\theta} = \frac{3a^{8} + 96a^{4}\rho^{4} - 256\rho^{8}}{32a^{6}\rho^{2}}$$

证:设W( − cos θ,  − sin θ),a = 2,则$XY = CZ = \tan\theta,c = WZ = 1 + \sec\theta,b = CX = 1 + \sqrt{1 - \tan^{2}\theta},\ \frac{b^{2} + c^{2}}{b + c} = \frac{4 + 2\sec\theta + 2\sqrt{1 - \tan^{2}\theta}}{2 + \sec\theta + \sqrt{1 - \tan^{2}\theta}} = 2 = a$.