求锐角△ABC中边AC的取值范围

baxiannv

在 $\triangle A B C$ 中，$A B=1$，$D$ 为 $B C$ 边上一点，且 $\angle A D B=\frac{\pi}{3}$ ．
（1）若 $A D$ 为 $B C$ 边上的中线，求边 $A C$ 的最大值；$\sqrt{3}$
（2）若 $A D$ 为 $\angle B A C$ 的平分线，且 $\triangle A B C$ 为锐角三角形，求边 $A C$ 的取值范围．$(2,2+\sqrt{3})$

kuing

（1）中线时：

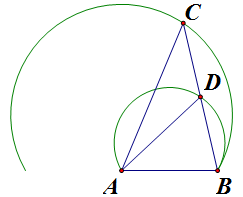
如上图，固定 `A`, `B`，因为 `\angle DAB=60\du` 且 `D` 为 `BC` 中点，故 `D`, `C` 两点的轨迹分别是小的圆弧和大的圆弧（两倍的大小），易知当 `AC\perp AB` 时 `AC` 最大，为 `\sqrt3`；

（2）角平分线时：

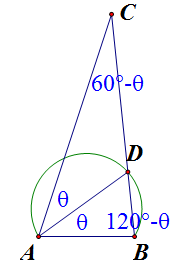
如上图，记 `\angle DAB=\theta`，由 `\triangle ABC` 为锐角三角形知 `\theta\in(30\du,45\du)`，由正弦定理有
\begin{align*}
AC&=\frac{\sin(120\du-\theta)}{\sin(60\du-\theta)}\\
&=\frac{\sin60\du\cos(60\du-\theta)+\cos60\du\sin(60\du-\theta)}{\sin(60\du-\theta)}\\
&=\frac{\sqrt3}2\cot(60\du-\theta)+\frac12,
\end{align*}
可见 `AC` 关于 `\theta` 递增。

当 `\theta=30\du` 时代入上式得 `AC=2`；

当 `\theta=45\du` 时代入上式得 `AC=\frac{\sqrt3}2\cot15\du+\frac12`。

还得算一下 `\cot15\du`，这里可以再用一下图形，由上图可知，当 `\theta=45\du` 时 `AC\perp AB` 且 `\angle C=15\du`，那么 `AC=\cot15\du`，于是有
\[\frac{\sqrt3}2\cot15\du+\frac12=\cot15\du \riff \cot15\du=\frac1{2-\sqrt3}=2+\sqrt3.\]
综上，`AC` 的范围是 `\bigl( 2,2+\sqrt3 \bigr)`。

nttz

回复 2# kuing

1.为什么c的轨迹是圆弧？
2.如果题目中不是锐角三角形呢？

kuing

回复 3# nttz

1. B 是定点，D 轨迹是圆弧，`\vv{BC}=2\vv{BD}`，所以 C 轨迹也是圆弧，而且是两倍大小。
2. 不限制锐角三角形的话 `\theta` 就可以趋向 60°，AC 就无限大了，另一方面 `\theta\to0` 时 AC 趋向下确界 1，因此范围就是 (1,+oo)

nttz

回复 4# kuing
1用到什么定理啊