正方形中求阴影面积(小学奥数吧)——数据需修正

isee

如图正方形中，$CG\perp BF$，数据如图，求红色阴影部分面积和. （个人认为的答案在图片描述里）

kuing

那两块的面积都是 `S_3` 是因为由垂直有 `\S{ABF}=\S{BCG}`，于是
\[S_1+S_2+2S_3+12=S_{ABCD}=2\S{FBC}=2(S_3+12),\]
即 `S_1+S_2=12`。

kuing

回复 1# isee

怎么用了我加字母之后的图

乌贼

如图：
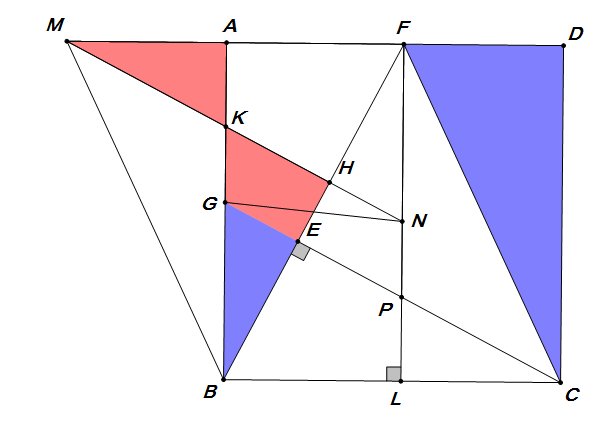
$ BM\px CF,MN\px CE $\[
\ S_{\triangle MFN}=\dfrac{1}{2}S_{BAFL}=S_{AFNG}\riff S_{\triangle MAK}=S_{\triangle NGK} \]又平行四边形$ KNPG $中\[S_{\triangle MAK}= S_{\triangle NKG}=\dfrac{1}{2}S_{KNPG}=S_{KHEG} \]有\[ S_{\triangle CDF}+S_{\triangle BED}=S_{\triangle BAM}+S_{\triangle BED}=S_{\triangle BHM}=S_{\triangle CEF}=12 \]

isee

但是，EF／EC＝2／3时，图形不存在，知乎的 xiaomm8341 说。

也是的，若记GE＝x，BE＝y，则有
$y^2=6x,6+x=y+4$此方程组无实数根，从而EF／EC取不到2／3.

即数据需修改

kuing

回复 6# isee

还真没去考虑这个问题
去掉 4、6，直接给出中间那块的面积即可