伪内切圆学习

hbghlyj

nl.wikipedia.org/wiki/Menglineair_ingeschreven_cirkel
Constructie
De menglineair ingeschreven cirkel in hoek $A$, dus rakend aan $AB$ en $AC$ kan als volgt worden geconstrueerd:

• $I$ is het middelpunt van de ingeschreven cirkel van $ABC$ en
• $AI$ is de bissectrice van hoek $A$.
• $T$ is het punt waar een lijn vanuit $I$ loodrecht op $AI$ de zijde $AC$ snijdt.
• $Ma$ is weer het snijpunt van een loodlijn uit $T$ op bissectrice $AI$.
• De cirkel met middelpunt $Ma$ door $T$ is de gevraagde cirkel.

De straal $ρ_A$ van de menglineair ingeschreven cirkel in hoek $A$ is $ρ_A=\frac r{\cos^2 \frac \alpha 2}$, met $r$ de straal van de ingeschreven cirkel.
构造
角 $A$ 的伪内切圆，与 $AB$ 和 $AC$ 相切，可构造如下：

• $I$ 是 $ABC$ 的内心
• $AI$ 是角 $A$ 的平分线.
• $T$ 是过 $I$ 垂直于 $AI$ 的直线与边 $AC$ 相交的点.
• $Ma$ 是过 $T$ 的垂线与 $AI$ 平分线的交点。
• 中心为 $Ma$ 过 $T$ 的圆是所求的圆。

角$A$的伪内切圆的半径$ρ_A$是$ρ_A=\frac r{\cos^2 \frac \alpha 2}$，其中$r$是内切圆的半径。

hbghlyj

Eigenschappen
De lijnen, die een hoekpunt verbinden met het raakpunt van de corresponderende menglineaire ingeschreven cirkel en omgeschreven cirkel, snijden elkaar in één punt. Het gezamenlijke snijpunt is het driehoekscentrum met Kimberlingnummer $X(55)$, het uitwendig gelijkvormigheidscentrum van de ingeschreven cirkel en de omgeschreven cirkel.

Deze drie lijnen snijden elkaar nog steeds in één punt, wanneer in de hele berekening in plaats van de omgeschreven cirkel van $ABC$ een andere, willekeurige cirkel wordt genomen.

将顶点连接到相应的伪内切圆和外接圆的切点的线相交于一点。共同的交点是Kimberling三角形中心$X(55)$，内切圆和外接圆的外相似中心。 如果在整个计算过程中采用另一个任意圆而不是 $ABC$ 的外接圆，这三条线仍然在一个点相交。

hbghlyj

forumgeom.fau.edu/FG2006volume6/FG200601.pdf
mathworld.wolfram.com/MixtilinearIncircles.html
web.evanchen.cc/handouts/Mixt-GeoGuessr/Mixt-GeoGuessr.pdf
services.artofproblemsolving.com/download.php … aW5jaXJjbGVzLnBkZg==
awesomemath.org/wp-pdf-files/math-reflections … 2020_mixtilinear.pdf
bilibili.com/read/cv5051453
zhuanlan.zhihu.com/p/75211920
okazakiyumemi.github.io/blog/伪内切圆专题学习/

hbghlyj

mathoe.com/dispbbs.asp?boardid=88&id=44699
设△ABC的外接圆为ω，圆Γ与AB 、AC、△ABC的外接圆ω分别相切于E、F、K。则E、F与△ABC的内心I共线。
这题是1993第34届国际数学奥林匹克IMO备选题（西班牙供题），也称曼海姆（Mannheim）定理。
下面这个另法证明用到了外心、内心之间的欧拉（Euler）心距公式OI＝R^2－2Rr和斯特瓦特（Stewart）定理。

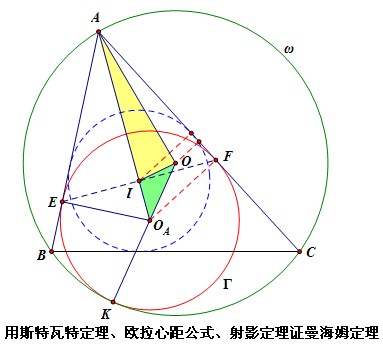
证明: 设 $\triangle A B C$ 的外心为 $O$, 外接圆半径为 $R$; 内心为 $I$, 内切圆半径为 $r ; \angle B A C$ 的伪内 切圆圆心为 $O_{A}$, 半径为 $\rho \circ \angle B A C=\alpha, \angle A B C=\beta, \angle B C A=\gamma$ a 则 $A I=\frac{r}{\sin \frac{\alpha}{2}}$, $A O_{A}=\frac{\rho}{\sin \frac{\alpha}{2}}, I O_{A}=A O_{A}-A I=\frac{\rho}{\sin \frac{\alpha}{2}}-\frac{r}{\sin \frac{\alpha}{2}}=\frac{\rho-r}{\sin \frac{\alpha}{2}} \cdot \therefore \frac{I O_{A}}{A O_{A}}=\frac{\rho-r}{\rho}(1)_{\mathrm{a}}$ 在 $\triangle A O O_{A}$ 中使用斯特瓦特 (Stewart) 定理: $A I \cdot O O_{A}^{2}+O_{A} I \cdot A O^{2}=A O_{A} \cdot O I^{2}+A I \cdot O_{A} I \cdot A O_{A}$, 代入数 据, $\frac{r}{\sin \frac{\alpha}{2}} \cdot(R-\rho)^{2}+\frac{\rho-r}{\sin \frac{\alpha}{2}} \cdot R^{2}=\frac{\rho}{\sin \frac{\alpha}{2}} \cdot{\sqrt{R^{2}-2 R r}}^{2}+\frac{r}{\sin \frac{\alpha}{2}} \cdot \frac{\rho-r}{\sin \frac{\alpha}{2}} \cdot \frac{\rho}{\sin \frac{\alpha}{2}}$, 整理, 得 $\left(\sin \frac{\alpha}{2}\right)^{2}=\frac{\rho-r}{\rho}(2)$, 由(1)(2)可得, $\frac{I O_{A}}{A O_{A}}=\frac{\rho-r}{\rho}=\left(\sin \frac{\alpha}{2}\right)^{2}=\left(\frac{\rho}{A O_{A}}\right)^{2}$, $\therefore O_{A} I \cdot O_{A} A=\rho^{2}=O_{A} F^{2}$, 而 $\angle A F O_{A}=90^{\circ}$, 由射影昰理逆昰理, 则 $A O_{A} \perp E F$, 又 $A E=$ $A F, \therefore A O_{A}$ 还平分 $E F$, 即 $I 、 E 、 F$ 三点共线, 且 $I$ 是 $E F$ 的中点。
注: 此证明中用到了外心、内心之间的欧拉 (Euler) 心距公式 $O I=\sqrt{R^{2}-2 R r}$ 和斯特瓦特 (Stewart) 定理。

hbghlyj

设△ABC 的外接圆为ω，圆Γ与 AB 、AC、△ABC 的外接圆ω分别相切于 E、F、K。则 E、F 与△ABC 的内心 I 共线。

证明：延长KE交△ABC的外接圆⊙O于点M，则点CM平分∠ACB，延长KF交△ABC的外接圆⊙O于点N，则BN平分∠ABC，在⊙O的圆内接六边形ABNKMC（这个六边形不是凸的）中，由帕斯卡（Pascal）定理，其三组对边（AB，KM），（BN，CM），（NK，CA）的交点E、I、F三点共线。
由切线长定理，AE＝AF，即I还平分EF，AI⊥EF。
_______________________
延长KE交△ABC的外接圆⊙O于点M，则点CM平分∠ACB。

证明：过点K作两圆的公切线ST，则弦切角∠SKP＝∠KQP，∠SKB＝∠KAB，
∴PQ∥AB，∴弧EQ＝弧EP，∴∠EKP＝∠EKQ，即∠MKB＝∠MKA，
即弧MB＝弧MA，即∠MCB＝∠MCA，即MC过△ABC的内心I，
同理BN也过△ABC的内心I。