|
|
Last edited by hongxian 2013-6-15 18:432013湖北文22,理21
感觉能变圆,有人能秒吗?
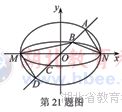
如图,已知椭圆$C_1$,$C_2$的中心在坐标原点$O$,长轴均为$MN$且在$x$轴上,短轴长分别为$2m$,$2n$($m>n$),过原点且不与$x$轴重合的直线$l$与$C_1$,$C_2$的四个交点按纵坐标从大到小依次为$A$、$B$、$C$、$D$,记$\lambda=\frac m n$,$\triangle BDM$和$\triangle ABN$的面积分别为$S_1$和$S_2$
(1)当直线$l$与$y$轴重合时,若$S_1=\lambda S_2$,求$\lambda$的值;
(2)当$\lambda$变化时,是否存在与坐标轴不重合的直线$l$,使$S_1=\lambda S_2$?并说明理由
|
|