摄像校正

hbghlyj

ams.org/publicoutreach/feature-column/fc-2013-03
假设你想给这张平面拍照，
它在三维空间中。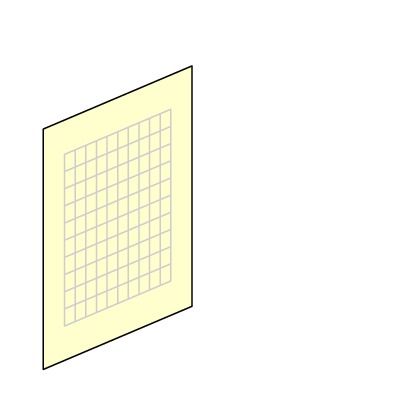
如果相机与平面恰好对齐，
那么图像将被均匀地缩放。
但是，如果相机的平面不平行于图像的平面，
那么平面的图像会被扭曲。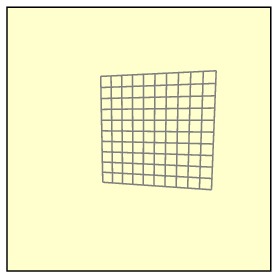
我们的目标是从相机记录的失真图像重建原始图像。
首先，我们将描述将一个平面投影到另一个平面的变换。 我们是考虑从平面到相机平面上的投影，还是从相机平面到原始平面的逆投影，这一点是无关紧要的。

假设我们将点 ${\bf p}$ 投影到方程 ${\bf n}\cdot {\bf x} = C$ 所描述的平面上。 下图显示了这个问题的二维版本。
我们将通过点 ${\bf p}$ 和眼睛$\bf eye$的直线上的点参数化为 ${\bf r} = (1-t){\bf p} + t{\bf eye}$ ，并询问何时该点位于平面${\bf n}\cdot {\bf x} = C$上。$${\bf n}·\Big((1-t){\bf p} + t{\bf eye}\Big)=C$$
解得 $$ t = \frac{C-{\bf n}\cdot {\bf p}}{{\bf n}\cdot{\bf eye} -{\bf n}\cdot {\bf p}}, $$

因此 $$ {\bf r} = \frac{{\bf n}\cdot{\bf eye} - C}{{\bf n}\cdot{\bf eye}-{\bf n}\cdot { \bf p}} {\bf p} + \frac{C- {\bf n}\cdot{\bf p}}{{\bf n}\cdot{\bf eye} - {\bf n}\cdot {\bf p}} {\bf eye} $$
如果写出平面上的坐标，就会发现函数的形式为 $$ (x,y)\mapsto(u,v) = \left(\frac{ax+by+c}{gx + hy + j }, \frac{dx + ey + f}{gx+hy+j}\right).$$
给定我们的两张图像，我们将选择失真图像中的四个点和校正图像中的四个对应点，并从这些数据中重建函数。
这个函数，称为射影变换。 尽管分量是有理函数，但分子和分母只是线性的。 出于这个原因，很自然地将这个函数重新定义为射影平面的变换，所谓射影平面就是${\bf R}^3$ 中穿过原点的直线的集合。
通过将欧氏平面置于 ${\bf R}^3$ 内作为平面 $z=1$，并将每一点对应到经过它和原点的直线，我们建立了从欧几里得平面到射影平面的一个嵌入，因为一条线与平面 $z=1$ 相交至多一点。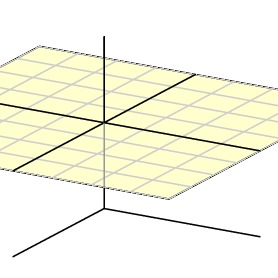
射影平面中的点使用齐次坐标来描述，我们将投影平面中的一条线表示为 $[x,y,z]$，其中 $(x,y,z)$ 是线上的一个点。请注意，$(x,y,z)$ 的任何标量倍数也是这条线上的一个点，即，仅相差标量倍数的两个点对应的齐次坐标是相同的。也就是说，$[x,y,z] = [wx,wy,wz]$。

请注意，欧几里得平面中的点形如 $[x,y,1]$。射影平面中的其他点形如 $[x,y,0]$，并且对应于位于 $xy$-平面中的直线。这些点有时被称为“无穷远点”，因为这样的点是欧几里得平面中无界的点序列的极限。

如果我们采用齐次坐标，我们可以将我们的变换写成 $$ [x,y,1]\mapsto [u,v,1] = [ax+by+c, dx+ey+f, gx+hy+j],$$

每个分量都是线性的，我们将看到，这带来了极大的方便。确定变换需要我们确定由常数 $a, b,\ldots, j$ 形成的矩阵。然而，由于使用齐次坐标，相差标量倍数的两个矩阵相同。

hbghlyj

本楼用于将行内的图片在竖直方向上,中线与文本对齐(vertical-align:middle)

本文中多次出现了“up to”,翻译成中文后很别扭 ,见zhihu.com/question/20906778
意思就是“只在乎三个坐标的比值”,所以“整体乘以标量后不变”,或者说“只相差一个标量因子,则视为相同”

hbghlyj

一个明显的解决方案

我们的问题并不是特别困难，它有一个简单的解决方案，我们现在将对其进行描述。

左边的图像称为源空间，右边的图像称为目标空间。 给定源空间中的四个点${\bf s}_i = (x_i, y_i)$，以及它们在目标空间中变换下的像${\bf t}_i=(u_i, v_i)$。 我们的目标是确定射影变换。
我们有 $$ \left[x_i \quad y_i \quad 1 \right] \left[\begin{array}{ccc} a & d & g \\ b & e & h \\ c & f & j \end{array} \right] = w_i\left[u_i \quad v_i \quad 1\right], $$

其中 $w_i=gx_i + hy_i + j$ 是比例因子。换句话说，  \[ \begin{eqnarray*} ax_i + by_i + c & = & w_i u_i \\ dx_i + ey_i + f & = & w_i v_i \\ gx_i + hy_i + j & = & w_i \end{eqnarray*} \]

即 \[ \begin{eqnarray*} ax_i + by_i + c & = & (gx_i+hy_i + j) u_i \\ dx_i + ey_i + f & = & (gx_i+hy_i + j) v_i \end{eqnarray*} \]

即 \[ \begin{eqnarray*} x_ia + y_ib + c -x_i u_i g - y_i u_i h - u_i j & = & 0 \\ x_id + y_ie + f -x_i v_i g - y_i v_i h - v_i j & = & 0 \end{eqnarray*} \]

即 \[\left[ \begin{array}{ccccccccc} x_i & y_i & 1 & 0 & 0 & 0 & -x_i u_i & - y_i u_i & - u_i \\ 0 & 0 & 0 & x_i & y_i & 1 & -x_i v_i & - y_i v_i & - v_i \end{array} \right] \left[\begin{array}{c} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \\ j \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]. \]


用四对点 $\{{\bf s}_i\}$ 和 $\{{\bf t}_i\}$，我们得到一个 $8\times 9$ 齐次方程组，它能确定常数 $a ,b,\ldots,j$ (相差标量倍数的两个矩阵确定的射影变换相同)。这就解释了为什么我们需要四对点来确定射影变换。

得到的变换可以表示为矩阵 $$ {\bf M_{st}} = \left[\begin{array}{ccc} a & d & g \\ b & e & g \\ c & f & j \end{array}\right] $$。

这是问题的明显解决方案。计算上，求解一个 $8\times9$ 的方程组有点令人不快，但并不太难。最严重的抱怨可能是，我们忽略了对问题的任何几何直觉。

hbghlyj

分成两步来做

一个更有趣的解决方案

与其寻找将点 ${\bf s}_i$ 直接转换为 ${\bf t}_i$ 的变换，不如构建一个到中间点集，单位正方形的顶点 ${\bf q}_i$ 的两步过程 。 也就是说，我们做映射

${\bf s}_i$	$\mapsto$	${\bf q}_i$	$\mapsto$	${\bf t}_i$

我们定义变换 ${\bf M_{sq}}$ 和 ${\bf M_{qt}}$ 使得 ${\bf s}_i{\bf M_{sq}}={\bf q}_i$ 和${\bf q}_i{\bf M_{qt}} = {\bf t}_i$。我们的最终目标是复合映射 $$ {\bf M_{st}} = {\bf M_{sq}} {\bf M_{qt}} $$。 但是请注意，${\bf M_{sq}} = {\bf M^{-1}_{qs}}$，而求出 ${\bf M_{qs}}$ 与求出$ {\bf M_{qt}}$基本上是相同的任务。 以上想法很有帮助，因为单位正方形的顶点坐标有很多零：$(0,0)$、$(1,0)$、$(1,1)$ 和 $(0,1) $，这导致方程更简单。例如，由于 ${\bf q}_0 = (0,0)$，其中两个方程是 \[\left[ \begin{array}{ccccccccc} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & - u_0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & - v_0 \end{array} \right] \left[\begin{array}{c} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \\ j \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right ] \]。 事实上，Blinn 展示了如何根据坐标 ${\bf t}_i = (u_i, v_i)$ 显式求解这八个方程以找到变换 ${\bf M_{qt}}$。该解决方案不是特别漂亮，但所需的计算工作量相对较少。 然后我们有 \[\begin{eqnarray*} {\bf M_{st}} & = & {\bf M_{sq}} {\bf M_{qt}} \\ & = & {\bf M^{- 1}_{qs}} {\bf M_{qt}}\end{eqnarray*} \]。 我们可以将 ${\bf M^{-1}_{qs}}$ 替换为它的伴随矩阵 ${ \bf M^*_{qs}}$，因为它们只差 $\det{\bf M_{qs}}$ 倍。我们得出 $$ {\bf M_{st}} = {\bf M^*_{qs}} {\bf M_{qt}}$$。

hbghlyj

重心坐标

Blinn 还描述了 Microsoft Research 的同事 Kirk Olynyk 发现的解决此问题的第二种方法，他使用重心坐标来简化计算。我们将首先描述重心坐标，然后描述 Olynyk 方法。

平面上有三个不共线的点${\bf p}_0$、${\bf p}_1$和${\bf p}_2$，我们可以将平面上的任意点${\bf p }$ 唯一地表为 $$ {\bf p} = \pi_0 {\bf p}_0 + \pi_1 {\bf p}_1 + \pi_2 {\bf p}_2, $$其中$\pi_0,\pi_1,\pi_2$满足 $\pi_0+\pi_1+\pi_2 = 1$。这是因为，式子等价于$$ {\bf p-p_0} = π_1({\bf p_1-p_0})+ π_2 ({\bf p_2-p_0}), $$现在，平面上一点$\bf p-p_0$可以唯一表为两点${\bf p_1-p_0},{\bf p_2-p_0}$的线性组合，这是显而易见的。证毕。

如果我们将重心坐标应用于目标空间中的一个点，我们有  \[ \begin{eqnarray*} \tau_0 {\bf t}_0 + \tau_1 {\bf t}_1 + \tau_2 {\bf t}_2 & = & {\bf t} \\ \left[\begin{array}{ccc} \tau_0 & \tau_1 & \tau_2 \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array} \right] & = & \left[\begin{array}{ccc} u & v & 1 \end{array}\right], \end{eqnarray*} \]

同样对于源空间中的一个点，我们有：$$ \sigma_0 {\bf s}_0 + \sigma_1 {\bf s}_1 + \sigma_2 {\bf s}_2 = {\bf s} $$。

现在考虑我们的变换 ${\bf M_{st}}$ 对重心坐标的影响。 \[\begin{eqnarray*} w{\bf t} & = & {\bf s}{\bf M_{st}} \\ w \left[\begin{array}{ccc} \tau_0 & \tau_1 & \tau_2 \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array} \right] & = & \left[\begin{array}{ccc} \sigma_0 & \sigma_1 & \sigma_2 \end{array}\right] \left[\begin{array}{ccc} x_0 & y_0 & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \end{array} \right]{\bf M_{st}} \\ \left[\begin{array}{ccc} w\tau_0 & w\tau_1 & w\tau_2 \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array} \right] & = & \left[\begin{array}{ccc} \sigma_0 & \sigma_1 & \sigma_2 \end{array}\right] \left[\begin{array}{ccc} w_0u_0 & w_0v_0 & w_0 \\ w_1u_1 & w_1v_1 & w_1 \\ w_2u_2 & w_2v_2 & w_2 \\ \end{array} \right] \\ \left[\begin{array}{ccc} w\tau_0 & w\tau_1 & w\tau_2 \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array} \right] & = & \left[\begin{array}{ccc} w_0\sigma_0 & w_1\sigma_1 & w_2\sigma_2 \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array} \right] \\ \end{eqnarray*} \]

表明 $$ \left[\begin{array}{ccc} w\tau_0 & w\tau_1 & w\tau_2 \end{array}\right] = \left[\begin{array}{ccc} w_0\sigma_0 & w_1\sigma_1 & w_2\sigma_2 \end{array}\right] $$

这表明变换 ${\bf M_{st}}$ 对重心坐标的影响是简单的乘法：$w\tau_i = w_i\sigma_i$。一旦我们确定了常数 $w_0$、$w_1$ 和 $w_2$，我们可以使用 $\tau_0+\tau_1+\tau_2 = 1$ 找到 $w$。

那么我们如何确定 $w_0$、$w_1$ 和 $w_2$？还记得吗，我们有第四对点 ${\bf s}_3$ 和 ${\bf t}_3$ 并且 ${\bf s}_3{\bf M_{st}} = {\bf t}_3$。如果我们将 ${\bf s}$ 的重心坐标写为 $[\tilde{\sigma}_0 \quad \tilde{\sigma}_1\quad\tilde{\sigma}_2]$ 和 $ {\bf t}$的重心坐标 $[\tilde{\tau}_0 \quad \tilde{\tau}_1\quad\tilde{\tau}_2]$，那么我们有，(最多差一个缩放常数)，$$ w_i = \frac{\tilde{\tau}_i}{\tilde{\sigma}_i} $$。

换句话说，在重心坐标中，变换 ${\bf M_{st}}$ 简单地由对角矩阵 $$ w[\tau_0 \quad \tau_1 \quad \tau_2] = [\sigma_0 \quad \sigma_1\quad \sigma_2] \left[ \begin{array}{ccc} \frac{\tilde{\tau}_0}{\tilde{\sigma}_0} & 0 & 0 \\ 0 & \frac{\tilde{\tau}_1}{\tilde{\sigma}_1} & 0 \\ 0 & 0 & \frac{\tilde{\tau}_2}{\tilde{\sigma}_2} \\ \end{array}\right]$$给出。

其中 $\tilde{\sigma}_i$ 和 $\tilde{\tau}_i$ 分别是 ${\bf s}_3$ 和 ${\bf t}_3$ 的重心坐标。

这是 ${\bf M_{st}}$ 的一个特别简单的表达式。但是请注意，找到 ${\bf s}$ 的重心坐标需要做一些额外的工作\[\begin{eqnarray*} [\sigma_0 \quad \sigma_1 \quad \sigma_2] \left[\begin{array}{ccc} x_0 & y_0 & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \end{array}\right] & = & [x \quad y \quad 1 ] \\ [\sigma_0 \quad \sigma_1 \quad \sigma_2] & = & [x \quad y \quad 1 ] \left[\begin{array}{ccc} x_0 & y_0 & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \end{array}\right]^{-1} \end{eqnarray*} \]
然后从$\bf t$的重心坐标求出目标点${\bf t}$。

总而言之，变换 ${\bf s}\mapsto{\bf t}$ 可以分下面几步来求出

• 求 ${\bf s}$ 的重心坐标，
• 计算 $w\tau_i = (\tilde{\tau}_i/\tilde{\sigma}_i) ~ \sigma_i$,
• 将坐标归一化，使得 $\tau_0+\tau_1+\tau_2 = 1$,
• 从$\bf t$的重心坐标求出 ${\bf t}$。

重心坐标的方法与“构造中间点集”的方法在精神上相似，两者都使用中间步骤来找到变换 ${\bf M_{st}}$。 前者首先转换为重心坐标再将 ${\bf M_{st}}$ 分解为单独缩放。后者将 ${\bf M_{st}}$ 分解为两个变换，借助一组过渡的点，即单位正方形的顶点。

hbghlyj

Blinn 的最终改进

下面是 Blinn 发现的第三种方法，其简单性令人惊叹。与第一种方法相同地，通过一组中间点 ${\bf b}_i$ 分解 ${\bf M_{st}}$。然而，我们将不使用单位正方形，而是选择射影平面中的点，使其具有尽可能多的零： \[\begin{eqnarray*} {\bf b}_0 & = & [1\quad 0 \quad0] \\ {\bf b}_1 & = & [0\quad 1 \quad0] \\ {\bf b}_2 & = & [0\quad 0 \quad1] \\ {\bf b}_3 & = & [1\quad 1 \quad1] \\ \end{eqnarray*} \]

请注意，其中两个点是无穷远点，但这有什么不对的呢？为了描述变换 ${\bf M_{bt}}$，请注意 ${\bf b}_i {\bf M_{bt}} = {\bf t}_i = [w_i u_i\quad w_iv_i\quad w_i] .$ 考虑前三个点 ${\bf b}_0$、${\bf b}_1$ 和 ${\bf b}_2$，我们发现 \[ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right] {\bf M_{bt}} = \left[\begin{array}{ccc} w_0u_0 & w_0v_0 & w_0 \\ w_1u_1 & w_1v_1 & w_1 \\ w_2u_2 & w_2v_2 & w_2 \\ \end{array}\right] \]。

由此，我们立即得到变换 ${\bf M_{bt}}$: $${\bf M_{bt}} = \left[\begin{array}{ccc} w_0u_0 & w_0v_0 & w_0 \\ w_1u_1 & w_1v_1 & w_1 \\ w_2u_2 & w_2v_2 & w_2 \\ \end{array}\right] = \left[\begin{array}{ccc} w_0 & 0 & 0 \\ 0 & w_1 & 0 \\ 0 & 0 & w_2 \\ \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right ] $$。

现在只需要找到 $w_0$、$w_1$ 和 $w_2$，我们可以使用第四点来完成：\[ \begin{eqnarray*} {\bf b}_3{\bf M_{bt} } & = & {\bf t}_3 \\ [1\quad1\quad1] \left[\begin{array}{ccc} w_0 & 0 & 0 \\ 0 & w_1 & 0 \\ 0 & 0 & w_2 \ \ \end{array}\right] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right] & = & [w_3u_3 \quad w_3v_3 \quad w_3] \\ [w_0\quad w_1\quad w_2] & = & w_3[u_3 \quad v_3 \quad 1] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right]^{-1} \end{eqnarray*} \]

在这里，我们看到与 Olynyk 方法的明确关系：$w_0$、$w_1$ 和 $w_2$ 只是 ${\bf t}_3$ 的重心坐标按 $w_3$ 缩放。 $$ [w_0\quad w_1\quad w_2] = w_3[\tilde{\tau}_0\quad \tilde{\tau}_1\quad \tilde{\tau}_2]。 $$

由于 ${\bf M_{bt}}$ 乘以一个常数倍后对应的射影变换不变，因此我们可以选择 $w_3$ 为我们希望的任何值。如果我们选择 $$ w_3 = \det \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right]， $$

然后我们到达$$ [w_0\quad w_1 \quad w_2] = [u_3 \quad v_3 \quad 1] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right]^* $$

使用目标数据，我们将定义矩阵 ${\bf T}$为 $$ {\bf T} = \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right], $$

所以 $$ [w_0\quad w_1 \quad w_2] = [u_3 \quad v_3 \quad 1] \quad {\bf T}^* $$

当然，我们仍然需要用类似的方式找到 ${\bf M_{sb}}$： $$ {\bf M_{bs}} = \left[\begin{array}{ccc} z_0 & 0 & 0 \\ 0 & z_1 & 0 \\ 0 & 0 & z_2 \\ \end{array}\right] {\bf S}, $$

其中$$ [z_0\quad z_1 \quad z_2] = [x_3 \quad y_3 \quad 1]\quad {\bf S}^* $$

${\bf S}$ 是目标数据形成的矩阵：$${\bf S} = \left[\begin{array}{ccc} x_0 & y_0 & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \end{array}\right]. $$

把所有东西放在一起，我们得到 \[\begin{eqnarray*} {\bf M_{st}} & = &{\bf M_{sb}}{\bf M_{bt}} \\ & = & {\bf M_{bs}^*} {\bf M_{bt}} \\ & = & S \left[\begin{array}{ccc} z_0 & 0 & 0 \\ 0 & z_1 & 0 \\ 0 & 0 & z_2 \\ \end{array}\right]^* \left[\begin{array}{ccc} w_0 & 0 & 0 \\ 0 & w_1 & 0 \\ 0 & 0 & w_2 \\ \end{array}\right]{\bf T}^* \\ & = & {\bf S} \left[\begin{array}{ccc} w_0z_1z_2 & 0 & 0 \\ 0 & z_0w_1z_2 & 0 \\ 0 & 0 & z_0z_1w_2 \\ \end{array}\right]{\bf T}^*. \end{eqnarray*} \]

最重要的是，Blinn 对 $w_i$ 和 $z_i$ 给出了简单的几何解释。回想一下 \[ \begin{eqnarray*} [w_0\quad w_1 \quad w_2] & = & [u_3 \quad v_3 \quad 1] \left[\begin{array}{ccc} u_0 & v_0 & 1 \\ u_1 & v_1 & 1 \\ u_2 & v_2 & 1 \\ \end{array}\right]^* \\ & = & [u_3 \quad v_3 \quad 1] \left[\begin{array}{ccc} v_1-v_2 & v_2-v_0 & v_0-v_1 \\ u_2-u_1 & u_0-u_2 & u_1-u_0 \\ u_1v_2-u_2v_1 & u_2v_0-u_0v_2 & u_0v_1-u_1v_0 \\ \end{array}\right], \end{eqnarray*} \]

这表明 \[\begin{eqnarray*} w_0 & = &(u_1-u_3)(v_2-v_3) - (u_2-u_3)(v_1-v_3) \\ w_1 & = &(u_2-u_3)(v_0-v_3) - (u_0-u_3)(v_2-v_3) \\ w_2 & = &(u_0-u_3)(v_1-v_3) - (u_1-u_3)(v_0-v_3). \end{eqnarray*} \]

这些表达式表明 $w_i$ 可以解释为由点 ${\bf t}_i$ 形成的三角形之一的有向面积的两倍。在下图中，绿色代表正区域，红色代表负区域。

hbghlyj

总结   

很难想象 ${\bf M_{st}}$ 有更简单表达式： $$ {\bf M_{st}} = {\bf S} \left[\begin{array}{ccc} w_0z_1z_2 & 0 & 0 \\ 0 & z_0w_1z_2 & 0 \\ 0 & 0 & z_0z_1w_2 \\ \end{array}\right]{\bf T}^*. $$

回想一下，${\bf S}$ 是由源数据 ${\bf s}_i$ 和 ${\bf T}$ 和目标数据 ${\bf t}_i$ 求出的，我们只需要计算 $ w_i$ 和 $z_i$，如上所示，这是一个简单的任务。

正如我们所见，我们可以通过求解一个 $8\times9$ 齐次方程组来找到 ${\bf M_{st}}$。然而，通过考虑问题的几何性质，${\bf M_{st}}$ 的形式越来越简单。


参考   
•    Jim Blinn, Inferring Transforms 发表于 Jim Blinn的专栏: 记号, 记号, 记号(Notation, Notation, Notation). Morgan Kaufmann. 2003
    像 Blinn 的所有专栏一样，这篇文章既清晰又有趣。
•    Paul Heckbert, 纹理映射和图像变形的基础(Fundamentals of Texture Mapping and Image Warping)。硕士论文，加州大学伯克利分校，1989。

hbghlyj

personal.math.ubc.ca/~cass/graphics/Perspective.pdf

$\cal A\kern -.1667em\lower.5ex M\kern -.125emS$数学成像(math imagery)专栏ams.org/publicoutreach/math-imagery/math-imagery