|
|
Last edited by player1703 2022-5-16 12:20
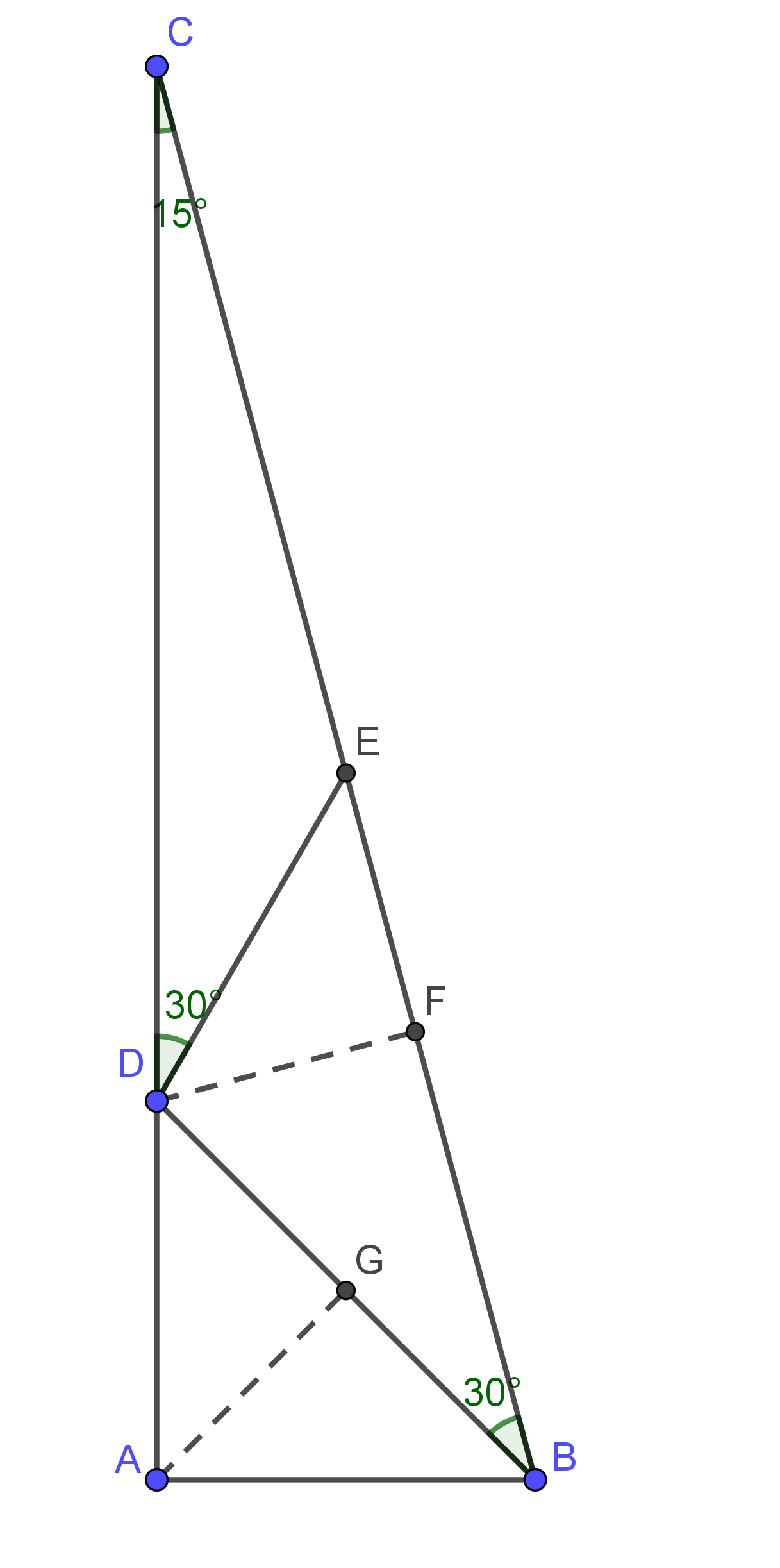
$\Rtt ABC$中$\angle A=90\du$, $\angle C=15\du$. $D$为直角边$AC$上一点且$AB=AD$. $\angle CDE = 30
\du$. 求证$DE=AD$.
当然我求助的是纯几何解法, 三角解法就简单了在$\triangle BDE$内用正弦定理得$\frac{DE}{\sin 30\du} = \frac{\sqrt{2}AD}{\sin 45\du}$
更新: 突然想到了直接把上面正弦定理的解法翻译成平几算几何法不?
过$D$作$DF\perp AB$于$F$, 取$BD$中点$G$连接$AG$. $DF=\frac{1}{2}BD=AG$ 所以等腰直角三角形$DFE$, $AGD$全等.
其实上面是我改的原来的题条件是$E$是$BC$中点我的解法如下:
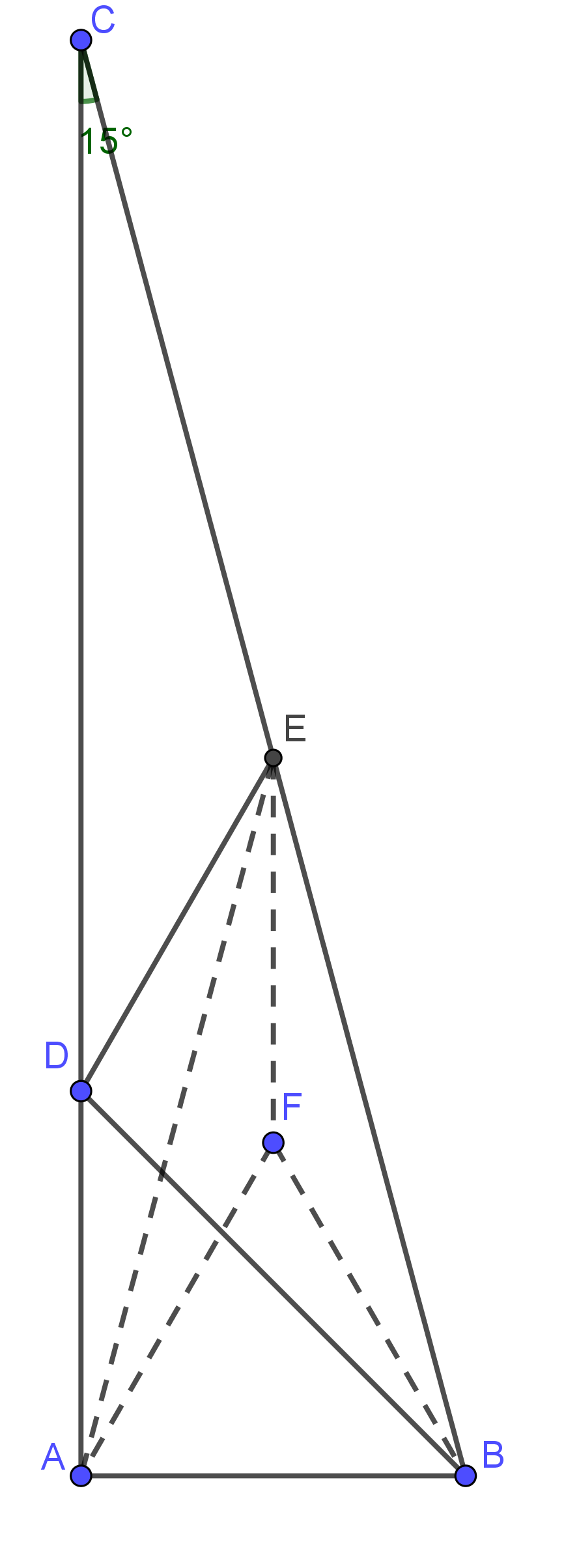
连接$AE$, 有$AE=BE$.以$AB$为底边向上作正三角形$AFB$. 显然$EF\perp AB$且$EF$平分$\angle AEB$. 故$EF\px DA$, 且$EF=AF=AB=AD$. 故ADEF是菱形.
|
|