圆的最佳Bezier逼近

hbghlyj

在Asymptote中,基本数据类型path是(分段)Bezier曲线

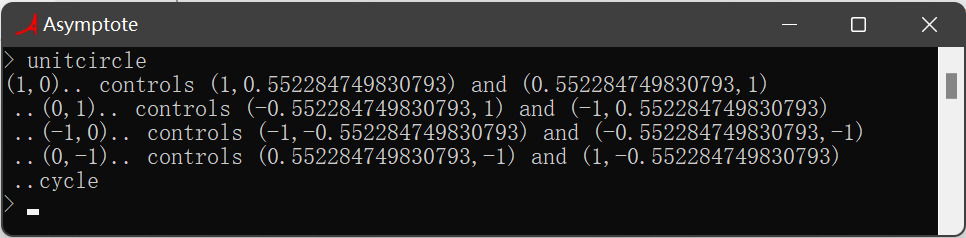
> unitcircle (1,0).. controls (1,0.552284749830793) and (0.552284749830793,1) ..(0,1).. controls (-0.552284749830793,1) and (-1,0.552284749830793) ..(-1,0).. controls (-1,-0.552284749830793) and (-0.552284749830793,-1) ..(0,-1).. controls (0.552284749830793,-1) and (1,-0.552284749830793) ..cycle > _

Windows下实际运行的屏幕截图:


那么,这个数是怎么得来的呢? 见spencermortensen.com/articles/bezier-circle/

Standard approximation

The standard approach imposes the following constraints:

• The endpoints of the cubic Bézier curve must coincide with the endpoints of the unit right circular arc, and their first derivatives must agree there.
• The midpoint of the cubic Bézier curve must lie on the circle.

The general form of a cubic Bézier curve is: $$\mathbf{B}(t)=(1-t)^{3} \mathbf{P}_{0}+3(1-t)^{2} t \mathbf{P}_{1}+3(1-t) t^{2} \mathbf{P}_{2}+t^{3} \mathbf{P}_{3}, t \in[0,1]$$ The first constraint implies that: $$\mathbf{P}_{0}=(0,1), \mathbf{P}_{1}=(c, 1), \mathbf{P}_{2}=(1, c), \mathbf{P}_{3}=(1,0)$$ And the second constraint provides the value of $c$: $$c=\frac{4}{3}(\sqrt{2}-1)$$ This gives the approximation: $$c≈0.55228474983079$$In this approximation, the Bézier curve remains outside the circle at all times, except momentarily when it dips in to touch the circle at its midpoint and endpoints:

hbghlyj

A better approximation

However, a better approximation is possible if we replace the final constraint with a new constraint:

• The endpoints of the cubic Bézier curve must coincide with the endpoints of the unit right circular arc, and their first derivatives must agree there.
• The maximum radial drift must be as small as possible.

This explicitly constrains the radial drift, resulting in a better fit.
The first constraint yields the parametric form of the cubic Bézier curve:\begin{array}{l}x(t)=3 c(1-t)^{2} t+3(1-t) t^{2}+t^{3} \\ y(t)=3 c t^{2}(1-t)+3 t(1-t)^{2}+(1-t)^{3}\end{array}…which gives the radial drift:$$d(t)=\sqrt{x^{2}+y^{2}}-1$$This function, $d(t)$, has minima at $t=0,\frac12,1$, and maxima at $t=\frac12±\frac{\sqrt{12-20c-3c^2}}{4-6c}$

hbghlyj

弧长