求正四面体在一个平面上的投影面积的取值范围

hbghlyj

求棱长为$\sqrt2$的正四面体在一个平面上的投影面积的取值范围.


设顶点为(0,0,1),(1,0,0),(0,1,0),(1,1,1)的正四面体绕$x$轴旋转$α$,再绕$y$轴旋转$β$后,投影到$x$-$y$平面上,先求出投影面积

area[x_] :=
  Module[{V = RotationTransform[β, {0, 1, 0}]@*RotationTransform[α, {1, 0, 0}] /@ x},
   Area[Polygon[ReplacePart[#, 3 -> 0] & /@ V]]];
{a, b, c, d} = {{0, 0, 1}, {1, 0, 0}, {0, 1, 0}, {1, 1, 1}};
area[{a, b, c, d}]
area[{a, b, d, c}]
area[{a, c, b, d}]得出
$S_1=|\sinβ|$
$S_2=|\cosα\cosβ|$
$S_3=|\sinα\cosβ|$
所以$S_1^2+S_2^2+S_3^2=1$
考虑两种情形:
当投影是四边形时,以上3种顺序之中有一个是凸四边形,面积最大(另外两个是折四边形).
当投影是三角形时,第四个顶点的投影在其内部.
这两种情形下,投影的面积$S$都可以表示为$S=\frac{S_1+S_2+S_3}2$
最大值
当投影是四边形时,$S=\max\{S_1,S_2,S_3\}$,而$S_1,S_2,S_3⩽1$,所以$S⩽1$.
当投影是三角形时,$S$就是一个三角形面$F$的投影面积,而$F$的投影面积⩽$F$的面积=$\frac{\sqrt3}2$,所以$S⩽\frac{\sqrt3}2$
所以最大值是$\frac{\sqrt3}2$,取等时投影为正三角形(投影面平行于$F$).
最小值
$S_1^2+S_2^2+S_3^2=1⇒\frac{S_1+S_2+S_3}2⩾\frac{1}{\sqrt{2}}$,当$S_1,S_2,S_3$之中有两个数=$\frac{1}{\sqrt{2}}$,第三个数=0时取等.(投影面平行于正四面体的一个二面角的平分面)
比如$α=\fracπ4,β=0$时,投影是

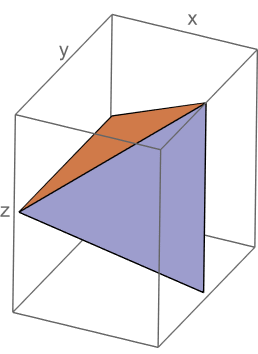
Graphics3D[{RotationTransform[Pi/4, {1, 0, 0}][
   Tetrahedron[{{0, 0, 1}, {1, 0, 0}, {0, 1, 0}, {1, 1, 1}}]]},
Ticks -> False, Axes -> True, AxesLabel -> {"x", "y", "z"},
ViewProjection -> "Orthographic"]

hbghlyj

应该有更直接的方法得出$S_1^2+S_2^2+S_3^2=1$?

换成正方体怎么解呢

Tesla35

zhihu.com/question/64435076/answer/220723396