Laplace's equation, Robin Boundary Problem

hbghlyj

courses.maths.ox.ac.uk/pluginfile.php/21926/m … ctures22.pdf#page=62
Corollary 105 (Robin (or Mixed) Boundary Problem) Let $R \subseteq \mathbb{R}^{3}$ be a path-connected region with piecewise smooth boundary $\partial R$ and let $f$ be a continuous function defined on $\partial R$. Further let $\beta$ be a real constant. Suppose that $\phi_{1}$ and $\phi_{2}$ are such that
\begin{align*}
\nabla^{2} \phi_{1} &=0=\nabla^{2} \phi_{2} \text { in } R \\
\beta \phi_{1}+\frac{\partial \phi_{1}}{\partial n} &=f=\beta \phi_{2}+\frac{\partial \phi_{2}}{\partial n} \text { on } \partial R .
\end{align*}
(i) If $\beta>0$ then $\phi_{1}=\phi_{2}$ in $R$.
(ii) If $\beta=0$ then $\phi_{1}-\phi_{2}$ is constant in $R$.
(iii) If $\beta<0$ then the solution need not be unique, even up to a constant.
Proof. Let $\psi=\phi_{1}-\phi_{2}$, so that
$$
\nabla^{2} \psi=0 \text { in } R, \quad \beta \psi+\frac{\partial \psi}{\partial n}=\beta \psi+\nabla \psi \cdot \mathbf{n}=0 \text { on } \partial R \text {. }
$$
If we consider the function $\psi^{2}$ then, by the Divergence Theorem and as $\nabla^{2}=\nabla \cdot \nabla$,
$$
\iint_{\partial R} \nabla\left(\psi^{2}\right) \cdot \mathrm{d} \mathbf{S}=\iiint_{R} \nabla^{2}\left(\psi^{2}\right) \mathrm{d} V
$$
Looking at the LHS and noting $\beta \psi+\nabla \psi \cdot \mathbf{n}=0$ on $\partial R$ we have
$$
\iint_{\partial R} \nabla\left(\psi^{2}\right) \cdot \mathrm{d} \mathbf{S}=\iint_{\partial R} 2 \psi(\nabla \psi \cdot \mathbf{n}) \mathrm{d} S=\iint_{\partial R} 2 \psi(-\beta \psi) \mathrm{d} S=-2 \beta \iint_{\partial R} \psi^{2} \mathrm{~d} S
$$
On the RHS we have as before
$$
\nabla^{2}\left(\psi^{2}\right)=2 \psi \nabla^{2} \psi+2 \nabla \psi \cdot \nabla \psi=2|\nabla \psi|^{2} \quad \text { as } \nabla^{2} \psi=0 \text { in } R
$$
Hence
$$
-2 \beta \iint_{\partial R} \psi^{2} \mathrm{~d} S=\iint_{R} 2|\nabla \psi|^{2} \mathrm{~d} V .
$$
If $\beta>0$ then the LHS is non-positive and the RHS is non-negative — consequently both are zero and $\nabla \psi=\mathbf{0}$ in $R$ and $\psi=0$ on $\partial R$. Hence $\psi=0$ throughout $R$.

If $\beta=0$ then the Robin Boundary Problem is just the Neumann Problem, with which we have already dealt.
The following example shows that solutions need not be unique if $\beta<0$.
Example 106 Let $R$ be the interior of the cylinder $x^{2}+y^{2}=1$. Find two solutions to the Robin Boundary Problem
$$
\nabla^{2} \psi=0 \text { in } R, \quad \psi=\frac{\partial \psi}{\partial n} \text { on } \partial R .
$$
Solution. Laplace's equation in cylindrical polars reads
$$
\nabla^{2} \psi=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \psi}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} \psi}{\partial \theta^{2}}+\frac{\partial^{2} \psi}{\partial z^{2}}=0 .
$$
We know for $\psi=r^{n} \sin n \theta$, where $n$ is a non-negative integer, that $\nabla^{2} \psi=0$ and on the boundary $r=1$ we have
$$
\frac{\partial \psi}{\partial n}=\frac{\partial \psi}{\partial r}=n r^{n-1} \sin n \theta=n \sin n \theta ; \quad \psi=\sin n \theta
$$
Hence when $n=1$, we see $r \sin \theta$ satisfies the given boundary problem. Other solutions are $0,r \cos \theta$ and $r \sin (\theta-\alpha)$ for arbitrary $\alpha$ so we see this solution is far from unique.

hbghlyj

I found document properties surprising: This is a 50.2MB file, but only 81 pages!

PDF Producer: Microsoft: Print To PDF

A file generated by 'Microsoft Print To PDF' can be 50 times larger than the original file.
Probably, the author produced the original PDF by pdfTeX, then added annotation (or correction...) using 'Microsoft Print To PDF'.
Also, the text isn't selectable (due to the format of embeded fonts?). From this answer:

... They are different. Saving as PDF yielded True Type fonts being embedded, whereas printing to PDF yielded True Type (CID) fonts. You can check in Properties and select the "Fonts" tab.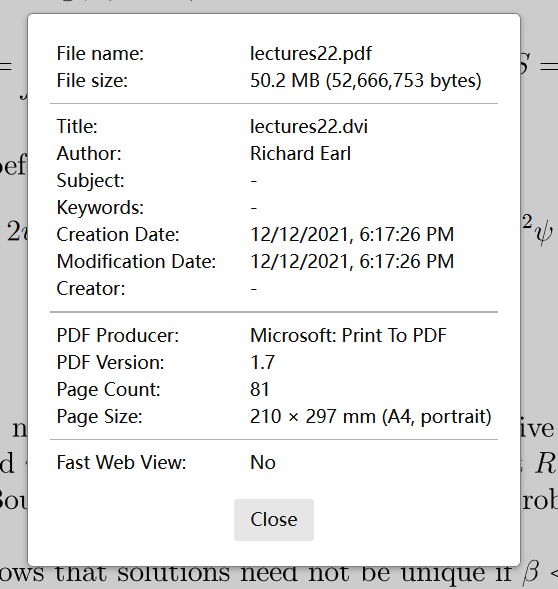