矩形中对轴求三角形面积最小值

isee

源自知乎提问





题：在矩形 ABCD 中 AB=6，BC=8，点 O 为其对称中心，点 E 在 AB 边上，连接 EO 并延长并 CD 于 F，将四边形 AEFD 沿 EF 翻折得到四边形 $A'EFD'$，边 $A'E$ 交 BC 于 G，则三角形 OGC 的面积最小值为____.

图 1

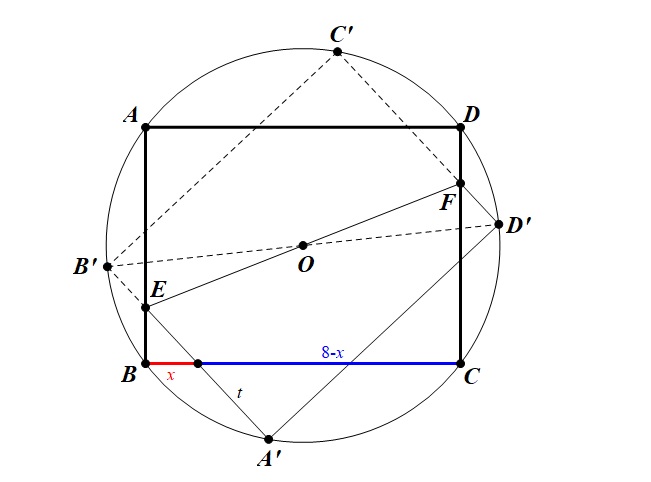
对称轴 EF 是过矩形中心 O 的，则将四边形 ABCD 沿 EF 轴对称得到 $A'B'C'D'$ ，则这八个点均在以 O 为圆心，直径为 10 的圆上，如图 1 标记，则在圆 O 中由相交弦定理，

知 $$x(8-x)=A'G\cdot GB'=t(6-t),$$

整理为关于 t 的二次方程 $$t^2-6t+8x-x^2=0,$$

则 $$\Delta=36-4(8x-x^2)\geqslant 0,$$

解得 $x\leqslant 4-\sqrt 7$，（由图形 $x<8-x$ 粗判断出 x<4），

从而 $S_{\triangle OGC}=\frac 12 \cdot GC\cdot 3=\frac 32(8-x)\geqslant \frac {12+3\sqrt 7}2.$

kuing

如上图，以 `O` 为圆心作一圆与 `AB` 相切，则 `A'E` 也与该圆相切，那么 `G` 能达到的最右的位置就是图中的交点 `H`，由切割线定理有 `BH\cdot(BC-BH)=BM^2` 即 `BH\cdot(8-BH)=9` 解得 `BH=4-\sqrt7`，从而 `GC\geqslant4+\sqrt7`，所以 `\S{OGC}\geqslant6+3\sqrt7/2`。

isee

kuing 发表于 2022-7-9 18:10
如上图，以 `O` 为圆心作一圆与 `AB` 相切，则 `A'E` 也与该圆相切，那么 `G` 能达到的最右的位置就是图中 ...

这解法也是绝了，反正以前都是没有见过的

kuing

isee 发表于 2022-7-9 18:16
这解法也是绝了，反正以前都是没有见过的

然而该解法发到那边也只有两个赞😌（即便加上了动图……

isee

kuing 发表于 2022-7-12 20:48
然而该解法发到那边也只有两个赞😌（即便加上了动图……

哈哈哈，浏览量跟不上~~无所谓啦~基本上100的浏览量才有一二赞