平行于任一平行线被其他三条射线截出两等线段

isee

源自知乎提问





题：若 PA，PQ 是圆 O 的切线，如图 1 所示，MH // PQ 交 AQ 于点 T，求证：HT = TM.





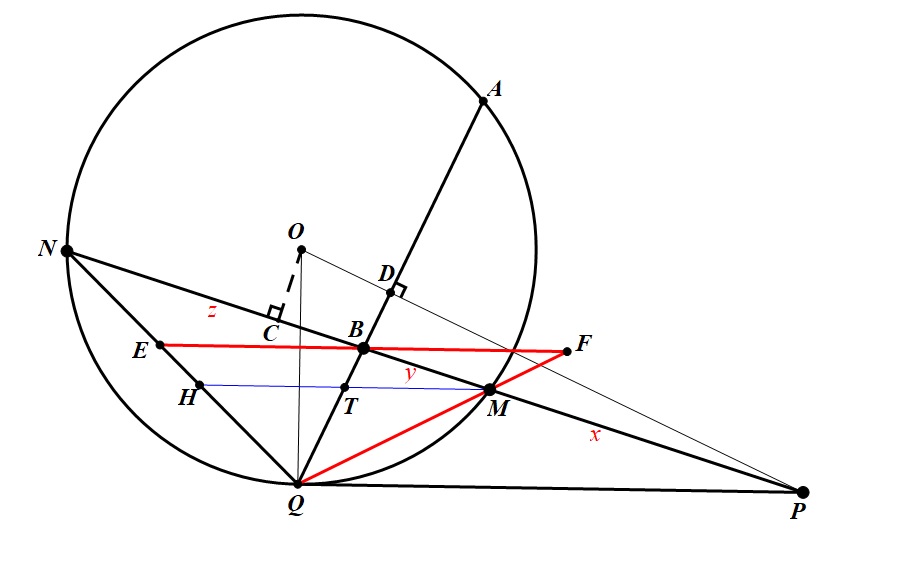
图 1



此答献给平面几何爱好者，特别是仅学习了义务教育规定的平面几何内容.



本证明是平几法，分两步：

第一步：证 $\frac {BM}{MP}=\frac {BN}{NP}.$ 第二步：过点 B 作 PQ 的平行线，如图 1，证 $EB=BF.$

第一步
过圆心作 OC 垂直于 MN 于 C 则 C 点 MN 的中点，连接 OP 交 AQ 于 D 则PO 垂直于 AQ，从而 O，C，B，D 四点共圆，由相交弦定理有

$PB\cdot PC=PD\cdot PO,$

另一方面在 Rt$\triangle OQP$ 中，由射影定理有

$PQ^2=PD\cdot PO,$

于是 $PB\cdot PC=PQ^2.$

在 $\odot O$ 中由切割线定理有

$PQ^2=PM\cdot PN,$

于是 $\bbox[lightblue,3pt]{PB\cdot PC=PM\cdot PN}$，

记 $PM=x,$ $MB=y,$ $BN=z$ 则上式(蓝色式子)变为

$(x+y)\cdot \left(x+\frac {y+z}2\right)=x(x+y+z),$ 展开合并整理即得

$xz=y(x+y+z)$ 即第一步完成： $\frac {BM}{MP}=\frac {BN}{NP}.$

第二步
过点 B 作 PQ 的平行线交 QN 于 E，交直线 QM于 F，如图 1 所示，则有

$\frac {BE}{PQ}=\frac {BN}{NP}=\frac {BM}{MP}=\frac {FB}{PQ}$，所以 $BE=BF$.

而 EF 与 HM 以 Q 点为位似中心，即有 $HT=TM.$

乌贼

如图：
$ B $为$ MN $中点，有$ PAOBQ $五点共圆。得\[ \angle BMT=\angle BPQ=\angle BAT \]所以$ BAMT $四点共圆，因此\[ \angle QNM=\angle QAM=\angle TBM\riff BT\px NQ\riff TM=TH \]

isee

乌贼 发表于 2022-7-26 03:06
如图：
$ B $为$ MN $中点，有$ PAOBQ $五点共圆。得\[ \angle BMT=\angle BPQ=\angle BAT \]所以$ BAMT $ ...

直切要害，漂亮！