在10到20的整数中,哪个不能表成连续正整数之和

hbghlyj

The only integer between 10 and 20 that is not the sum of consecutive positive integers?

Answer

5+6=11
3+4+5=12
6+7=13
2+3+4+5=14
7+8=15
16 is the number!
8+9=17
5+6+7=18
9+10=19

(However, if negative number is allowed, then no answer, as
–15 –14 –13 –12 –11 –10 –9 –8 –7 –6 –5 –4 –3 –2 –1 +0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16=16)

Full talk on YouTube

General Pattern

The sum of any two consecutive numbers is an odd number:
We need to look at the sum of consecutive numbers
$n+(n+1)=2n+1$
$n+(n+1)+(n+2)=3n+3$
$n+(n+1)+(n+2)+(n+3)=4n+6$
…
The sum of $x$ consecutive numbers is $xn+\frac{x(x-1)}2$.
We wish to find all numbers between 1 and 100 that is not the sum of consecutive numbers.

	For $x≥15$ we have $\frac{x(x-1)}2>100$. So 14 is an upper bound for $x$.
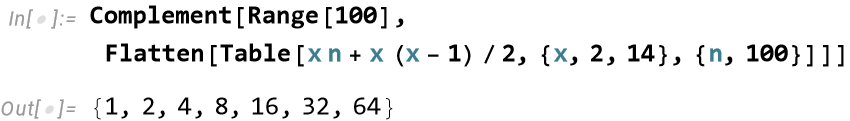
	We found a general pattern: $2^n,n∈\Bbb N$.

Proof

If $x$ is odd	$\displaystyle x=\frac{x-1}2+\frac{x+1}2$
If $\frac x2$ is odd	$\displaystyle x=\frac{\frac x2-3}2+\frac{\frac x2-1}2+\frac{\frac x2+1}2+\frac{\frac x2+3}2$
⋯	⋯
If $\frac x{2^n}$ is odd	$\displaystyle x=\frac{\frac x{2^n}-2^{n+1}+1}2+⋯+\frac{\frac x{2^n}+2^{n+1}-1}2$

If $x=2^n$ and $x=s+\dots+(s+k-1)=ks+\frac{k(k-1)}2$ where $k>1$,
then $2^{n+1}=k(2s+k-1)$, so $k=2^m,m≥1$,$$2s+k-1=2^{n-m+1}$$LHS is even but RHS is odd, contradiction.$\hspace1em\blacksquare$

Also see:
Prove that all even integers $n \neq 2^k$ are expressible as a sum of consecutive positive integers

Further question
In how many ways can a number be expressed as a sum of consecutive numbers?
将正整数$n$拆为连续正整数之和，要如何拆？