|
|
C. Smith, An Elementary Treatise on Conic Sections, Macmillan, London, 1885. pp. 226 (EXAMPLES ON CHAPTER X.)
59. With a fixed point for centre any circle is described cutting a conic in four points real or imaginary; shew that the locus of the centres of all conics through these four points is a rectangular hyperbola, which is independent of the radius of the circle.
[shew: old-fashioned spelling of ‘show’.]
设圆心为$(\alpha,\beta)$, 则经过圆与锥线的四个交点的任一锥线为$$a x^{2}+b y^{2}-1-\lambda\left\{(x-\alpha)^{2}+(y-\beta)^{2}-c^{2}\right\}=0$$| 求出中心的坐标并消去$\lambda$得$$b y (-x +α) + a x (y - β)=0$$ |
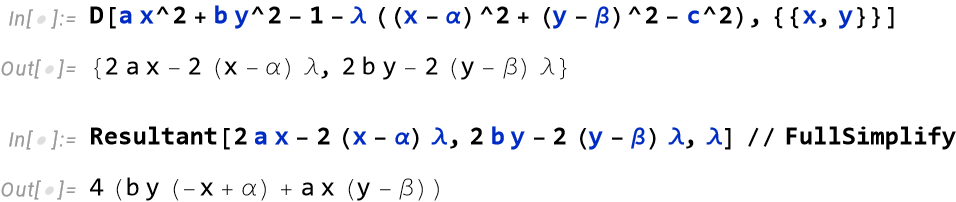
|
即$$xy=\frac{a \beta x-\alpha b y}{a-b}$$这是一条以$\left(-\frac{\alpha b}{a-b},\frac{a \beta }{a-b}\right)$为中心且经过原点的等轴双曲线, 且与圆的半径$c$无关.
Q.E.D |
|