三角形三极坐标下的圆

青青子衿

P为动点
外接圆、内切圆和九点圆的方程分别为：
\begin{gather*}
\left\{
\begin{split}
|BC|&=a\\
|AC|&=b\\
|AB|&=c\\
\end{split}
\right.\qquad
\left\{
\begin{split}
u&=a^{2}\left(b^{2}+c^{2}\right)-\left(b^{2}-c^{2}\right)^{2}\\
v&=b^{2}\left(a^{2}+c^{2}\right)-\left(a^{2}-c^{2}\right)^{2}\\
w&=c^{2}\left(a^{2}+b^{2}\right)-\left(a^{2}-b^{2}\right)^{2}\\
\end{split}
\right.\\
\\
\odot\>\!O\colon\quad
a^{2}\left(b^{2}+c^{2}-a^{2}\right)|PA|^{2}+b^{2}\left(a^{2}+c^{2}-b^{2}\right)|PB|^{2}+c^{2}\left(a^{2}+b^{2}-c^{2}\right)|PC|^{2}=2a^{2}b^{2}c^{2}\\
\\
\odot\>\!I\colon\quad
4\left(a|PA|^{2}+b|PB|^{2}+c|PC|^{2}\right)=4abc+\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)\\
\\
\odot\>\!N\colon\quad
2\left(u|PA|^{2}+v|PB|^{2}+w|PC|^{2}\right)=\left[4a^{2}b^{2}c^{2}+\left(a^{2}+b^{2}-c^{2}\right)\left(a^{2}+c^{2}-b^{2}\right)\left(b^{2}+c^{2}-a^{2}\right)\right]
\end{gather*}

kuing

我来推导一下。

（1）外接圆的：

由熟知的 `\sum\sin2A\cdot\vv{OA}=\bm0` 可得
\[\vv{PO}=\sum\frac{\sin2A}{\sin2A+\sin2B+\sin2C}\vv{PA},\]
为方便书写，将上式右边的三个系数分别记作 `x`, `y`, `z`，则 `x+y+z=1`，当 `P` 在外接圆上时，对上式两边平方得
\begin{align*}
R^2&=\left( \sum x\vv{PA} \right)^2\\
&=\sum x^2PA^2+2\sum xy\vv{PA}\cdot\vv{PB}\\
&=\sum x^2PA^2+\sum xy(PA^2+PB^2-AB^2)\\
&=\sum(x^2+xy+xz)PA^2-\sum xyAB^2\\
&=\sum xPA^2-\sum xyc^2,\quad(*)
\end{align*}
利用恒等式 `\sin2A+\sin2B+\sin2C=4\sin A\sin B\sin C` 可将 `x` 化为
\[x=\frac{\cos A}{2\sin B\sin C}=\frac{2R^2\cos A}{bc}=\frac{R^2(b^2+c^2-a^2)}{b^2c^2},\]
于是
\[\sum xPA^2=R^2\sum\frac{b^2+c^2-a^2}{b^2c^2}PA^2,\]
又
\[xyc^2=\frac{\cos A\cos B}{4\sin A\sin B\sin^2C}c^2=R^2\cot A\cot B,\]
于是
\[\sum xyc^2=R^2\sum\cot A\cot B=R^2,\]
代回前面的式 (*) 中约去 `R^2` 就是
\[1=\sum\frac{b^2+c^2-a^2}{b^2c^2}PA^2-1,\]
去分母就是
\[2a^2b^2c^2=\sum a^2(b^2+c^2-a^2)PA^2.\]

kuing

（2）内切圆的：

这就简单多了，仿楼上，有
\[\vv{PI}=\sum\frac a{a+b+c}\vv{PA},\]
记 `x=a/(a+b+c)` 等，当 `P` 在内切圆上时，楼上的式 (*) 的左边变成 `r^2`，也就是
\begin{align*}
r^2&=\sum xPA^2-\sum xyc^2\\
&=\frac{\sum aPA^2}{a+b+c}-\sum\frac{ab}{(a+b+c)^2}c^2\\
&=\frac{\sum aPA^2}{a+b+c}-\frac{abc}{a+b+c},
\end{align*}
而由面积公式有
\[r^2=\frac{4S^2}{(a+b+c)^2}=\frac{(a+b-c)(b+c-a)(c+a-b)}{4(a+b+c)},\]
代入上面即得
\[(a+b-c)(b+c-a)(c+a-b)=4\sum aPA^2-4abc.\]

kuing

（3）九点圆的：

不太了解相关量，有空再补😁

或者请楼主告诉我一下，九点圆半径公式，以及圆心 `N` 满足怎样的 `\sum(???)\vv{NA}=\bm0`？有这个照代 2# 的公式就成。

hbghlyj

kuing 发表于 2022-8-13 11:01
（3）九点圆的：

不太了解相关量，有空再补😁

九点圆与外接圆关于$H$ 1:2位似, 九点圆半径=$\frac R2$
The barycentric coordinates of the nine-point center are\begin{align*}
& a\cos(B-C):b\cos (C-A):c\cos (A-B) \\
= {} & a^2(b^2+c^2)-(b^2-c^2)^2:b^2(c^2+a^2)-(c^2-a^2)^2:c^2(a^2+b^2)-(a^2-b^2)^2.
\end{align*}
代回前面的式 (*) 中\begin{align*}
\frac{R^2}4&=\sum a\cos(B-C)PA^2-\sum ab\cos(B-C)\cos(C-A)c^2\\
&=\sum a\cos(B-C)PA^2-\frac{1}{2} abc\sum c\{\cos (A-B)-\cos (3C)\}
\end{align*}
@kuing 看看还能化简不

hbghlyj

近代的三角形几何学 第15页 (第2章 中点坐标与三极坐标)
例题
(A) 外接圆.
现在 $\rho=R, Q O=0, l \propto \sin 2 A$, 所以
$$
\sin 2 A \cdot r_{1}^{2}+\sin 2 B \cdot r_{2}^{2}+\sin 2 C \cdot r_{3}^{2}=4 \Delta ^\text {注(1)}
$$
(B) 内切圆
$$\rho=r, Q O^{2}=I O^{2}=R^{2}-2 R r, l \propto a $$
所以$$a r_{1}^{2}+b r_{2}^{2}+c r_{3}^{2}=2 \Delta(r+2 R)^\text {注(2)}$$
(C) 九点圆
$$
\rho=\frac{1}{2} R, Q O^{2}=\frac{1}{4} O H^{2}=\frac{1}{4} R^{2}-2 R \cos A \cos B \cos C^{注 (3)}
$$
因为九点圆圆心的 n. c. 是 $\cos (B-C), \cdots$, b. c. 是 $\sin A \cos (B-C), \cdots$, 所以
$$
l \propto \sin 2 B+\sin 2 C
$$
所以
$$
\sum(\sin 2 B+\sin 2 C) r_{1}^{2}=4 \Delta(1+2 \cos A \cos B \cos C)
$$

---

(1) 译者注: $2 R^{2}(\sin 2 A+\sin 2 B+\sin 2 C)=8 R^{2} \sin A \sin B \sin C=4 \Delta$.
(2) 译者注: $(a+b+c)\left(r^{2}+2 R r\right)=2 \Delta(r+2 R)$.
(3) 译者注: $2 R \cos A \cos B \cos C$ 应为 $2 R^{2} \cos A \cos B \cos C$.

hbghlyj

(*)式又见forum.php?mod=viewthread&tid=7640
forum.php?mod=viewthread&tid=3567
又见forum.php?mod=viewthread&tid=8933&pid=47360

Lemma$\newcommand\7{d_a}\renewcommand\v[1]{\mathbf{#1}}\newcommand\0{R}
\newcommand\8{d_b}
\newcommand\9{d_c}$
For any $\7$, $\8$ and $\9$ in $\mathbb R$ we have
$$\|\7\v u+\8\v v+\9\v w\|^2=\0^2(\7+\8+\9)^2-(a^2\8\9+b^2\7\9+c^2\7\8) $$

kuing

现在来补 4#，从头推。

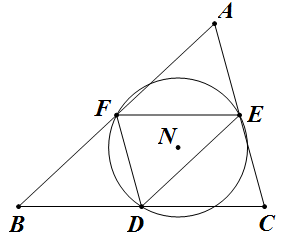
九点圆其实就是三边中点的外接圆，如上图，那么在 `\triangle DEF` 中就有
\[\sum\sin2D\cdot\vv{ND}=\bm0,\]
又显然 `\angle D=\angle A` 且 `2\vv{ND}=\vv{NB}+\vv{NC}`，上式就变成
\[\sum\sin2A\cdot\bigl(\vv{NB}+\vv{NC}\bigr)=\bm0,\]
也就是
\[\sum(\sin2B+\sin2C)\vv{NA}=\bm0,\]
由此得到
\[\vv{PN}=\sum\frac{\sin2B+\sin2C}{2(\sin2A+\sin2B+\sin2C)}\vv{PA},\]
将上式右边的三个系数记作 `x`, `y`, `z`，当 `P` 在九点圆上时，`PN=R/2`，仿照 2# 的式 (*)，就有
\[\frac14R^2=\sum xPA^2-\sum xyc^2,\quad(**)\]
现在来化简式 (**) 的两个和式，由
\begin{align*}
\sin2B+\sin2C&=\sin B\cdot2\cos B+\sin C\cdot2\cos C\\
&=\frac b{2R}\cdot\frac{a^2+c^2-b^2}{ac}+\frac c{2R}\cdot\frac{a^2+b^2-c^2}{ab}\\
&=\frac{a^2(b^2+c^2)-(b^2-c^2)^2}{2Rabc},
\end{align*}
以及
\[2(\sin2A+\sin2B+\sin2C)=8\sin A\sin B\sin C=\frac{abc}{R^3},\]
可知
\[x=\frac{R^2}{2a^2b^2c^2}\bigl( a^2(b^2+c^2)-(b^2-c^2)^2 \bigr),\]
但化简第二个和式就不用这个式子了，用回原定义，有
\begin{align*}
xy&=\frac{(\sin2B+\sin2C)(\sin2C+\sin2A)}{4(\sin2A+\sin2B+\sin2C)^2}\\
&=\frac{\sin2A\sin2B+\sin2C(\sin2A+\sin2B+\sin2C)}{4(\sin2A+\sin2B+\sin2C)^2}\\
&=\frac{4\sin A\cos A\sin B\cos B+8\cos C\sin A\sin B\sin^2C}{64\sin^2A\sin^2B\sin^2C}\\
&=\frac{\cot A\cot B}{16\sin^2C}+\frac{\cos C}{8\sin A\sin B},
\end{align*}
所以
\begin{align*}
\sum xyc^2&=\sum\left( \frac{R^2}4\cot A\cot B+\frac{R^2\cos C}{2ab}c^2 \right)\\
&=\frac{R^2}4\sum\left( \cot A\cot B+\frac{c^2(a^2+b^2-c^2)}{a^2b^2} \right)\\
&=\frac{R^2}4+\frac{R^2}{4a^2b^2c^2}\sum c^4(a^2+b^2-c^2),
\end{align*}
代回式 (**) 中，就是
\begin{align*}
\frac14R^2={}&\frac{R^2}{2a^2b^2c^2}\sum\bigl( a^2(b^2+c^2)-(b^2-c^2)^2 \bigr)PA^2\\
&-\frac{R^2}4-\frac{R^2}{4a^2b^2c^2}\sum c^4(a^2+b^2-c^2),
\end{align*}
去分母化简就是
\[2a^2b^2c^2+\sum c^4(a^2+b^2-c^2)=2\sum\bigl( a^2(b^2+c^2)-(b^2-c^2)^2 \bigr)PA^2,\]
又有恒等式
\[\sum c^4(a^2+b^2-c^2)=2a^2b^2c^2+\prod(a^2+b^2-c^2),\]
于是上上式再化为
\[4a^2b^2c^2+\prod(a^2+b^2-c^2)=2\sum\bigl( a^2(b^2+c^2)-(b^2-c^2)^2 \bigr)PA^2.\]

青青子衿

设$\>\triangle\>\!ABC\>$的外心为$\>O_{\triangle}\>$，点$\>P\>$为平面上的任意一动点，定点$\>Q\>$关于$\>\triangle\>\!ABC\>$的任意重心坐标为$\>\{l,m,n\}\>$，则有
\begin{gather*}
\odot\>\!Q\colon\quad
l|PA|^{2}+m|PB|^{2}+n|PC|^{2}=(l+m+n)\left(|PQ|^2+R_{\triangle}^2-|O_{\triangle}Q|^2\right)
\end{gather*}

旁切圆(Escribed circle)，又称外旁圆(Excircle)，该情况下的相关量
顶点$A$所对应的旁切圆圆心$J_A$的规范重心坐标为
\begin{align*}
\{\lambda,\mu,\nu\}&=
\left\{
\dfrac{-a}{b+c-a},
\dfrac{b}{b+c-a},
\dfrac{c}{b+c-a}\right\}
\end{align*}
\begin{align*}
r_{A}=|PJ_{A}|&=\dfrac{1}{2}\sqrt{\dfrac{(a+b+c)(a+b-c)(a+c-b)}{b+c-a}}\\
\big|O_{\triangle}J_{A}\big|&=\sqrt{R_{\triangle}^2+2R_{\triangle}r_{A}}
\end{align*}
伪内切圆(Pseudo inscribed circle)，又称混线内切圆(Mixtilinear incircle)，该情况下的相关量
顶点$A$所对应的伪内切圆圆心$K_A$的规范重心坐标为
\begin{align*}
\{\lambda,\mu,\nu\}&=
\left\{\dfrac{4 a b c-(a+b-c) (a+c-b) (a+b+c)}{(b+c-a) (a+b+c)^2}\right.,\\
&\qquad\quad\left.\dfrac{4 b^2 c}{(b+c-a) (a+b+c)^2},
\dfrac{4 b c^2}{(b+c-a) (a+b+c)^2}\right\}
\end{align*}
\begin{align*}
|PK_{A}|&=\frac{2bc}{a+b+c}\sqrt{\frac{(a+b-c)(a+c-b)}{(a+b+c)(b+c-a)}}\\
\big|O_{\triangle}K_{A}\big|&=R_{\triangle}-|PQ|
\end{align*}

青青子衿

Example 1.3.7 (Cocircularity of four points in the plane).
\begin{align*}
\odot\>\!O\colon\quad
a^{2}|PA|^{2}+b^{2}|PB|^{2}+c^{2}|PC|^{2}=2ab|PA||PB|+2ac|PA||PC|+2bc|PB||PC|\\
\end{align*}