|
|
Problemas-de-Geometría
Problem 334. Let $A B C$ be a triangle. For any point $P$, call $X Y Z$ its cevian triangle and $D E F$ its circumcevian triangle. The locus of points $P$ such that
$$
\frac{A D}{A X}+\frac{B E}{B Y}+\frac{C F}{C Z}=2
$$
is the cubic catalogued as K024 with equation
$$
b^{2} c^{2} x^{2} y+a^{2} c^{2} x y^{2}+b^{2} c^{2} x^{2} z+a^{2} c^{2} y^{2} z+a^{2} b^{2} x z^{2}+a^{2} b^{2} y z^{2}=0 .
$$
|
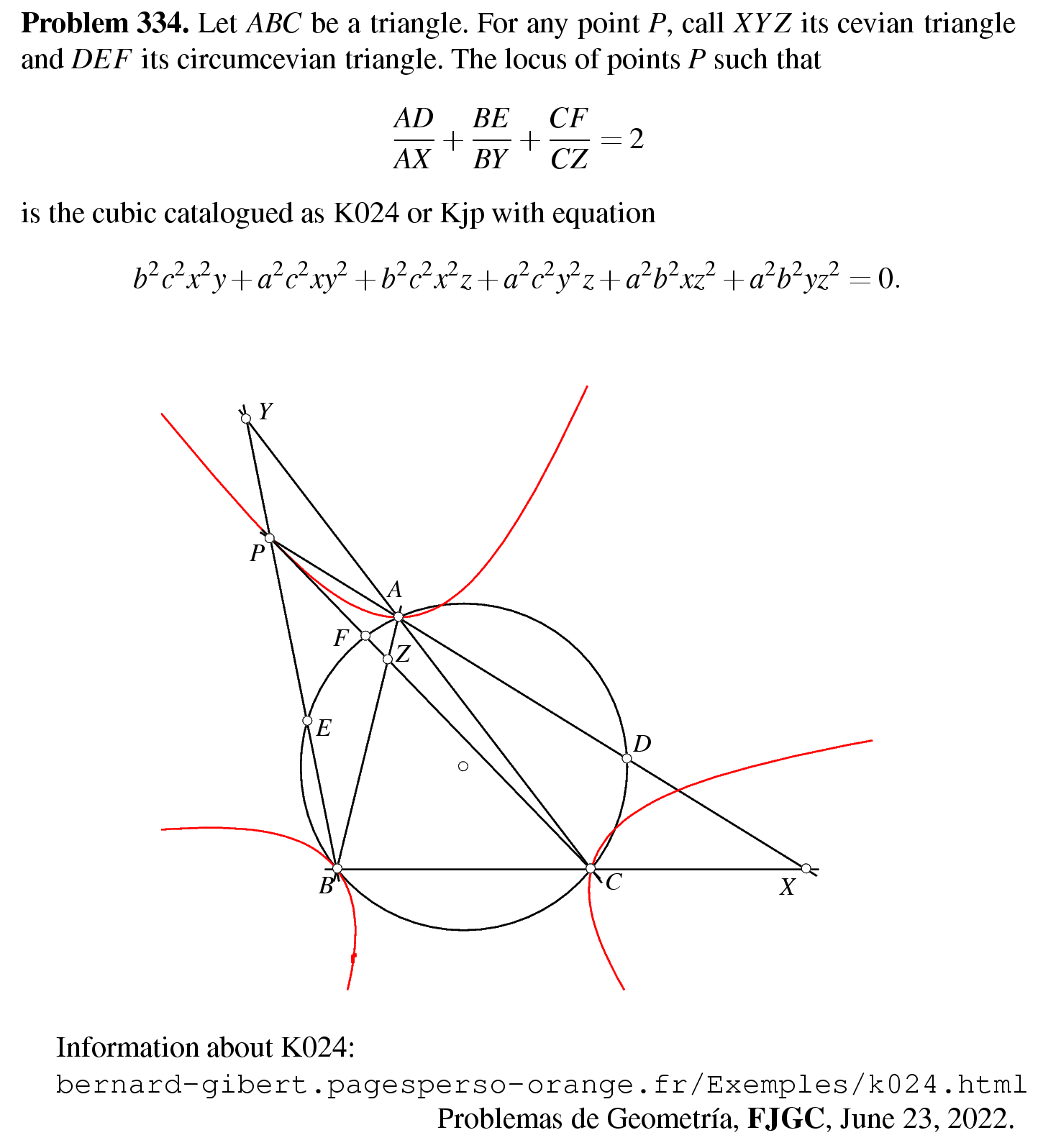
| A limit case for 334
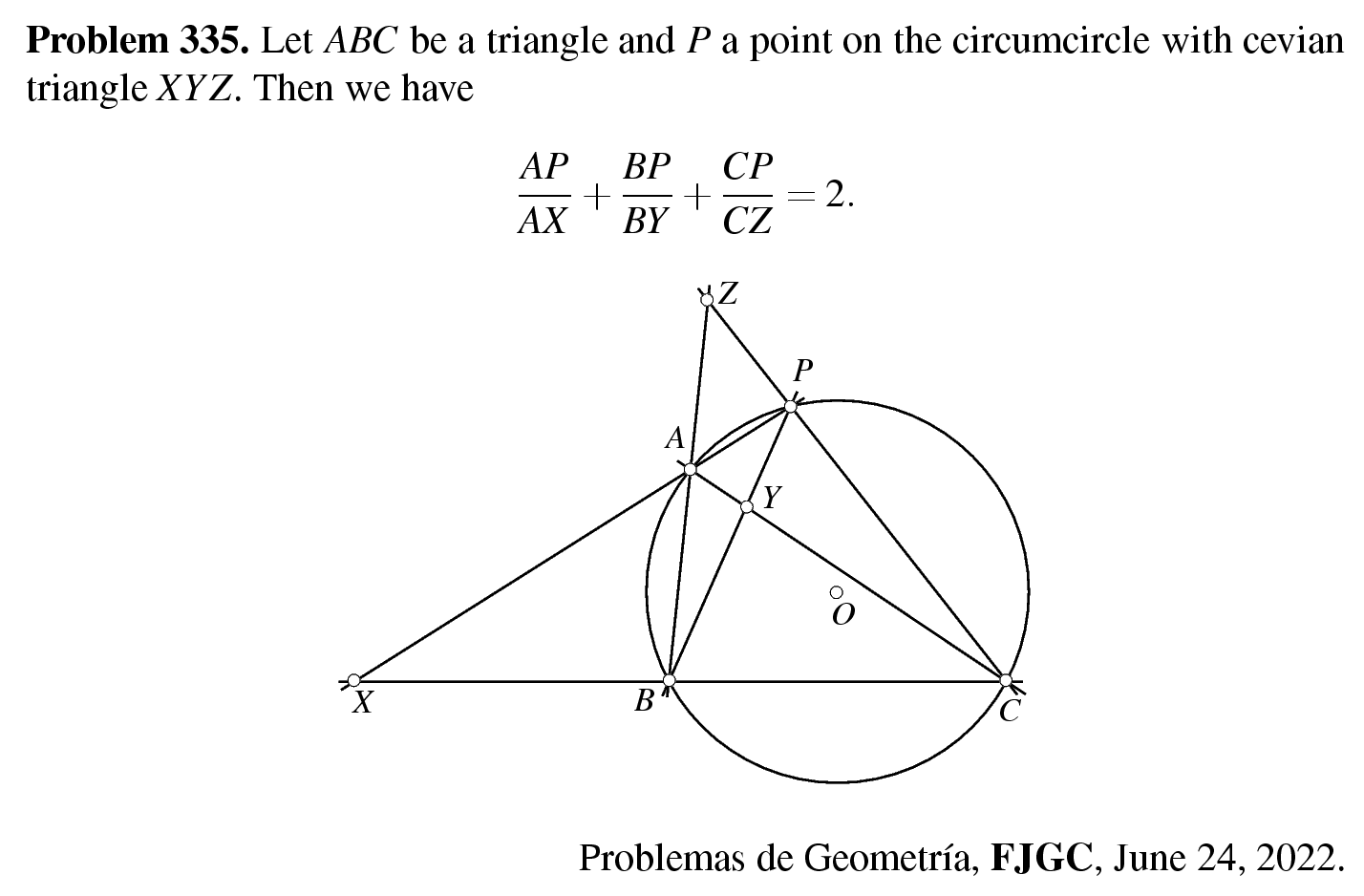
Problem 335. Let $A B C$ be a triangle and $P$ a point on the circumcircle with cevian triangle $X Y Z$. Then we have
$$
\frac{A P}{A X}+\frac{B P}{B Y}+\frac{C P}{C Z}=2 .
$$
|
|
Remark for 335.
If $P=(u: v: w)$ in homogeneous barycentric coordinates and $X Y Z$ is the cevian triangle of $P$ then we have
$$
\frac{P A}{A X}=-\frac{v+w}{u+v+w}, \quad \frac{P B}{B Y}=-\frac{w+u}{u+v+w}, \quad \frac{P C}{C Z}=-\frac{u+v}{u+v+w}
$$
therefore we have
$$
\frac{A P}{A X}+\frac{B P}{B Y}+\frac{C P}{C Z}=2
$$
for any point $P$. |
|