Pedagogical machine

hbghlyj

Kleppner Daniel, Kolenkow Robert, An Introduction to Mechanics (McGraw-Hill Science, 1973)(ISBN 0070350485)
Chapter 2, page 106

We shall demonstrate problem 2.20 using Mathematica.

hbghlyj

First let's solve the simultaneous equations for the pedagogical machine.

1. soln = Solve[{m1 ax1==F -T -N, m2 ax2 == T, m3 ax3 == N, m3 ay3 == T - m3 g, ax3 == ax1, ax2 - ax1 + ay3 == 0},{ax1,ax2,ax3,ay3,T,N}]

Copy the Code

\begin{array}{cc}
\text{ax1}\to -\frac{-F \text{m2}-F \text{m3}+g \text{m2} \text{m3}}{\text{m1}
   \text{m2}+\text{m1} \text{m3}+2 \text{m2} \text{m3}+\text{m3}^2} & \text{ax2}\to
   -\frac{-F \text{m3}-g \text{m1} \text{m3}-g \text{m3}^2}{\text{m1} \text{m2}+\text{m1}
   \text{m3}+2 \text{m2} \text{m3}+\text{m3}^2} \\
\text{ax3}\to -\frac{-F \text{m2}-F \text{m3}+g \text{m2} \text{m3}}{\text{m1}
   \text{m2}+\text{m1} \text{m3}+2 \text{m2} \text{m3}+\text{m3}^2} & \text{ay3}\to
   -\frac{-F \text{m2}+g \text{m1} \text{m3}+g \text{m2} \text{m3}+g
   \text{m3}^2}{\text{m1} \text{m2}+\text{m1} \text{m3}+2 \text{m2}
   \text{m3}+\text{m3}^2} \\
T\to \frac{\text{m2} \left(F \text{m3}+g \text{m1} \text{m3}+g
   \text{m3}^2\right)}{\text{m1} \text{m2}+\text{m1} \text{m3}+2 \text{m2}
   \text{m3}+\text{m3}^2} & N\to -\frac{-F \text{m2} \text{m3}-F \text{m3}^2+g \text{m2}
   \text{m3}^2}{\text{m1} \text{m2}+\text{m1} \text{m3}+2 \text{m2}
   \text{m3}+\text{m3}^2} \\
\end{array}Next get expressions for the accelerations for some particular choices of masses, and with $F=0$.

1. {ax1, ax2, ay3} /. soln /. {m1 -> 3, m2 -> 2, m3 -> 1, F -> 0, g -> 1}

Copy the Code

$$\left\{ -\frac{1}{7},  \frac{2}{7},  -\frac{3}{7} \right\}$$Define a function to produce the state of the machine, starting from rest at $t=0$.

1. state[t_] ={(-1/7),(2/7),(-3/7)} (1/2)t^2

Copy the Code

$$\left\{-\frac{t^2}{14},\frac{t^2}{7},-\frac{1}{14} \left(3 t^2\right)\right\}$$Define a function to draw the machine given its state.

1. machine[{x1_,x2_,y3_}]:= Show[Graphics[{RGBColor[1,0,0],Rectangle[{x1,0},{x1+2,2}],
2. Rectangle[{x1+2,0},{x1+3,(1/2)}],Rectangle[{x1+3,0},{x1+4,2}],
3. RGBColor[0,1,0],Rectangle[{x2,2},{x2+1,2+1/3}],RGBColor[0,0,1],Rectangle[{x1+2,3/2+y3},{x1+3,2+y3}]}],Axes->True,PlotRange->{{-1,4},{-1,4}},AspectRatio->1]

Copy the Code

For example at $t=0$, here is the picture: machine[{0, 0, 0}] Copy the Code
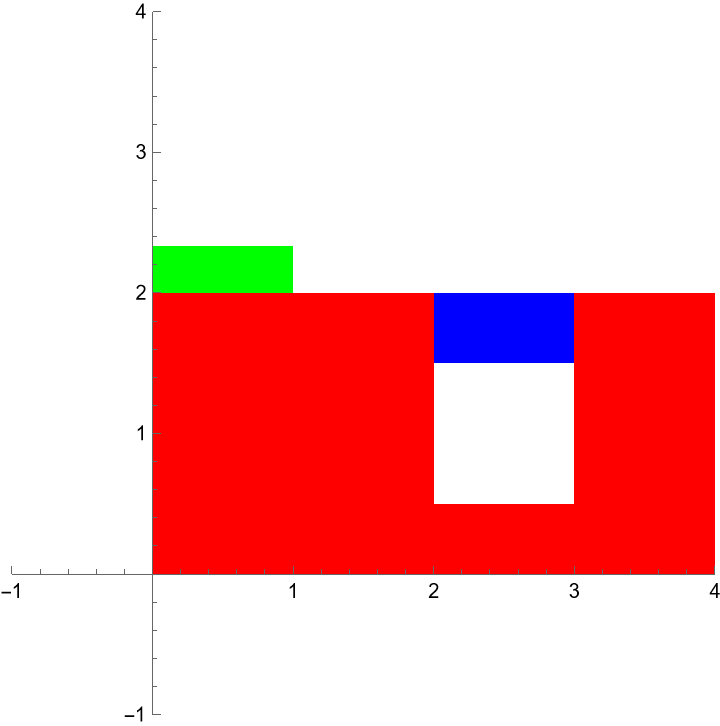
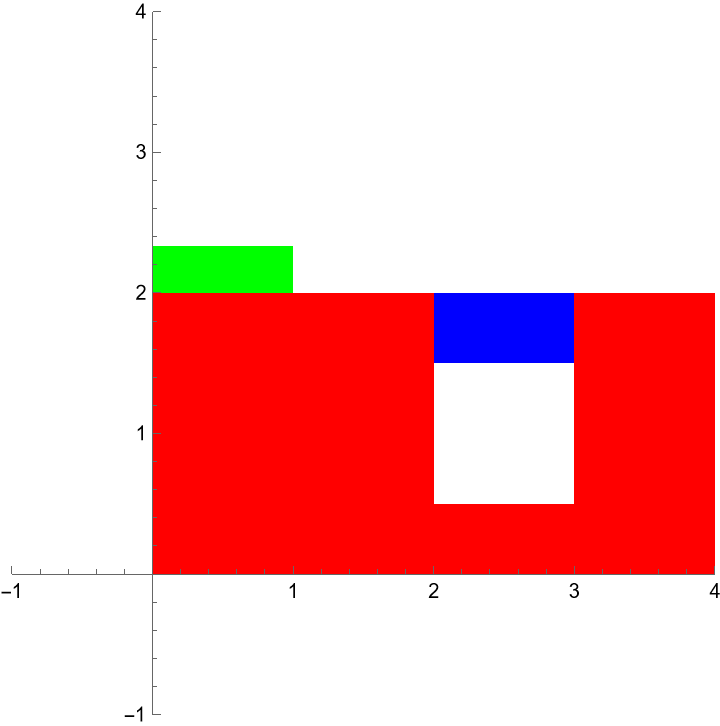
Finally, make a table of snapshots from $t=0$~$2$ and export as PNG. Export["D:\\pedmachine.png", Table[machine[state[t]], {t, 0, 2, .1}]] Copy the Code