|
|
几何变换 И. М. Ягло́м 美国新数学丛书 (译者: 詹汉生 章学诚) 北京大学出版社 1988 第二册 相似变换 第54页
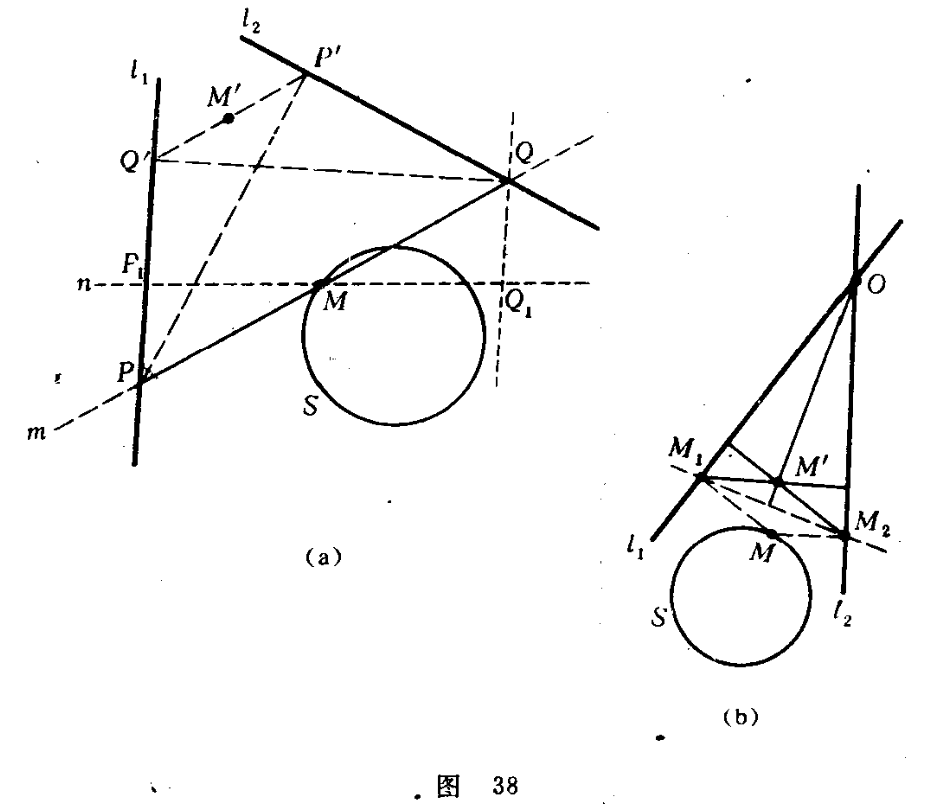
44.在平面上给定两条直线$l_1$和$l_2$,对平面上每个点$M$以如下的方式关联一个新的点$M'$.
(a)设$m$是过点$M$的直线,并且$m$介于$l_1$和$l_2$之间的线段$PQ$被$M$所平分.
设$P'$是$P$在$l_2$上的垂直投影,$Q'$是$Q$在$l_1$上的垂直投影,命$M'$是$P'Q'$的中点(图38(a))
(b)设$O$是$l_1,l_2$的交点,$M_1,M_2$分别是$M$在$l_1,l_2$上的投影,命$M'$是三角形$OM_1M_2$的垂心(图38(b))
现在假设$M$描出圆$S$,问$M$将描出什么样的轨迹?
我的想法
(a)显然$M$与$M'$关于$O$位似, 所以$M'$的轨迹为圆.
(b)设$M_1M$交$l_2$于$P$,由于$\triangle OM'P\sim\triangle OMM_1$,相似比为$OP/OM_1=\cos(l_1,l_2)$,所以$M'$关于$\angle M_1OM_2$的平分线的对称点与$M$关于$O$位似, 所以$M'$的轨迹为圆.

Mathematica 图片去除噪点 |
|