|
|
几何变换 И. М. Ягло́м 美国新数学丛书 (译者: 詹汉生 章学诚) 北京大学出版社 1988 第二册 相似变换 第50页
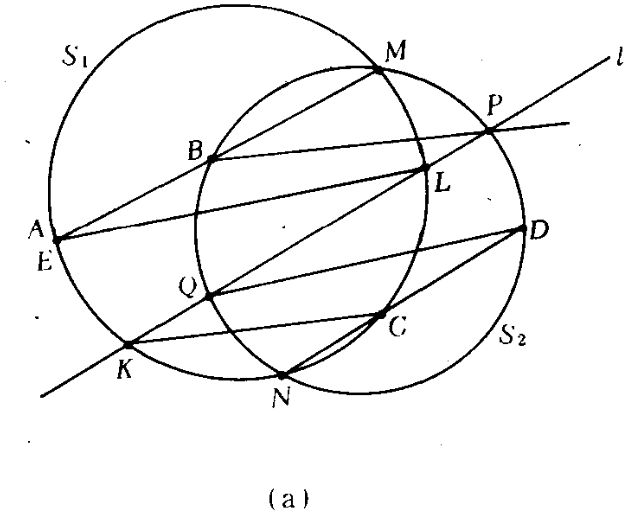
40.设$S_1$和$S_2$是相交于点$M$和$N$的两个圆,$l$是一条直线,$A$是$S_1$上的任意一点.
| (a) 设$l$与$S_1$交于点$K$和$L$,并且与$S_2$交于点$P$和$Q$〔图35(a)〕. 命$B$是直线$AM$与圆$S_2$的第二个交点,$C$是平行于$BP$的直线$KC$与$S_1$的第二个交点,$D$是直线$CN$与$S_2$的第二个交点. $E$是平行于$DQ$的直线$LE$与$S_1$的第二个交点. 证明$E$与$A$重合. |
|
如何证明呢 {:yiw}
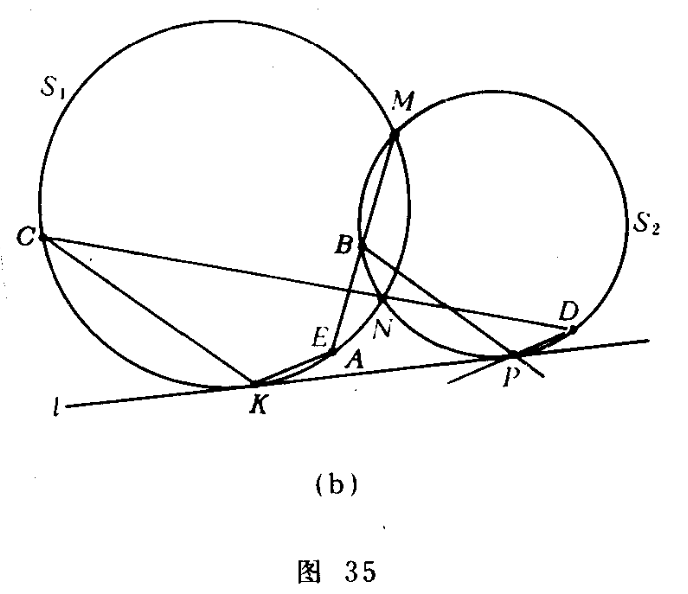
| (b) 设直线 $l$ 与 $S_1$ 和 $S_2$ 分别在点 $K$ 和 $P$ 相切〔图 35(b)〕. 命 $B$ 是直线 $A M$ 与 $S_2$ 的第二个交点, $C$ 是平行于 $B P$ 的直线 $K C$ 与 $S_1$ 的第二个交点, $D$ 是直线 $C N$ 与 $S_2$ 的第二个交点, $E$ 是平行于 $D P$ 的直线 $K E$ 与 $S_1$ 的第二个交点. 证明 $E$ 与 $A$ 重合. |
|
若我们移动直线$l$,使得点$K$与$L$重合,并且使得点$P$与点$Q$重合,即移动$l$使它成为$S_1$和$S_2$的公切线,则(a)的结果就变成(b)的结果。 |
|