零点分布的极限

hbghlyj

(Theoretical Physics 8) Wolfgang Nolting - Statistical Physics-Springer (2018) 4 Phase Transitions §4.6.4 Exercise 4.6.1
对于$0\le x\le 1$,
\begin{equation}\frac{1}{2}\left(\sqrt{z}+\frac{1}{\sqrt{z}}\right)+\sqrt{\frac{1}{4}\left(z+\frac{1}{z}\right)-\frac{1}{2}+x^{2}}=(-1)^{1 / N}\left\{\frac{1}{2}\left(\sqrt{z}+\frac{1}{\sqrt{z}}\right)-\sqrt{\frac{1}{4}\left(z+\frac{1}{z}\right)-\frac{1}{2}+x^{2}}\right\}\label1\end{equation}
其中$(-1)^{1 / N}=\exp \left(i \pi \frac{2 n-1}{N}\right) ; n=1,2, \ldots, N$.

证明: 方程\eqref{1}的零点$z_n$在单位圆上，且在垂直线 $\operatorname{Re}z=1-2x^2$ 的左侧。
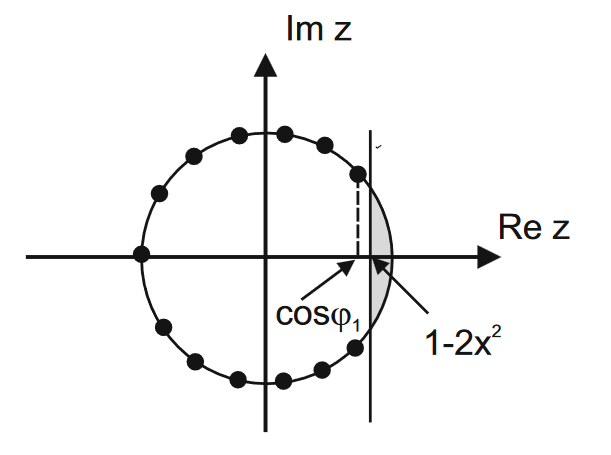
当$N\to\infty$时，零点越来越靠近，最终形成单位圆在垂直线 $\operatorname{Re}z=1-2x^2$ 的左侧的均匀覆盖。

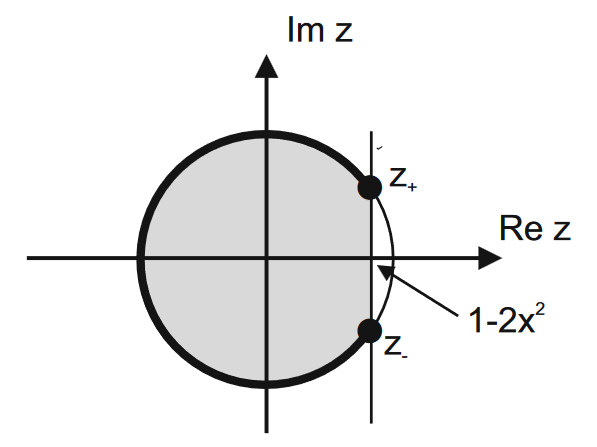
问题来源: The Yang-Lee zeros of the grand partition function

hbghlyj

令$$z_{n}=\exp \left(i \varphi_{n}\right)$$
然后可以使用：$$\frac{1}{2}\left(\sqrt{z}_{n}+\frac{1}{\sqrt{z}_{n}}\right)=\cos \left(\frac{\varphi_{n}}{2}\right)=\sqrt{\frac{1}{2}\left(1+\cos \varphi_{n}\right)}$$
得$$\frac{1}{4}\left(z_{n}+\frac{1}{z_{n}}\right)=\frac{1}{2} \cos \varphi_{n}$$
此外：
$$y_{n}=(-1)^{1 / N}=\exp \left(i \pi \frac{2 n-1}{N}\right) ; n=1,2, \ldots, N$$
方程\eqref{1}化为
$$\cos \left(\frac{\varphi_{n}}{2}\right)\left(1-y_{n}\right) =-\left(1+y_{n}\right) \sqrt{\frac{1}{2}\left(\cos \varphi_{n}-1\right)+x^{2}}$$
即
$$\frac{1}{2}\left(1+\cos \varphi_{n}\right)\left(1-y_{n}\right)^{2}=\left(1+y_{n}\right)^{2}\left(\frac{1}{2}\left(\cos \varphi_{n}-1\right)+x^{2}\right)$$
即$$\cos \varphi_{n}\left\{1-\frac{\left(1+y_{n}\right)^{2}}{\left(1-y_{n}\right)^{2}}\right\}=\frac{\left(1+y_{n}\right)^{2}}{\left(1-y_{n}\right)^{2}}\left(-1+2 x^{2}\right)-1$$即\begin{aligned} \cos \varphi_{n}\left\{-4 y_{n}\right\} &=\left(1+y_{n}\right)^{2}\left(-1+2 x^{2}\right)-\left(1-y_{n}\right)^{2} \\ &=-2\left(1+y_{n}^{2}\right)+2 x^{2}\left(1+y_{n}^{2}\right)+4 y_{n} x^{2} \\ &=-2\left(1-x^{2}\right)\left(1+y_{n}^{2}\right)+4 y_{n} x^{2} \end{aligned}即$$\cos \varphi_{n}=\frac{1}{2}\left(\frac{1}{y_{n}}+y_{n}\right)\left(1-x^{2}\right)-x^{2}$$因此\eqref{1}的根$$z_{n}=\exp \left(i \varphi_{n}\right) ; \quad \cos \varphi_{n}=\left(1-x^{2}\right) \cos \left(\pi \frac{2 n-1}{N}\right)-x^{2}$$位于单位圆上。
端点处的根满足：\begin{aligned} \cos \varphi_{\pm} &=1-2 x^{2} \\ \sin \varphi_{\pm} &=\pm \sqrt{1-\left(1-2 x^{2}\right)^{2}}=\pm 2 x \sqrt{1-x^{2}} \end{aligned}所以$$z_{\pm}=\left(1-2 x^{2}\right) \pm i 2 x \sqrt{1-x^{2}}$$