用FindRoot解方程组,然后RootApproximant

hbghlyj

下图中,由$APO$和$OP$来定义了一个中间变量$θ$,并试图用Solve解一个关于$APO$和$OP$的方程组,这个方程组有3个方程和2个变量.

过了很长时间出不来...我们就换成Eliminate来解...但是过了很长时间还是出不来...于是我们先求得一个近似解(如果原问题是几何题,可以用Geogebra画一下,手动调整,来获得一个近似解),然后使用FindRoot,并且把WorkingPrecision设为100

于是我们获得了一个数值解,精确度是小数点后100位.现在使用RootApproximant,试图获得精确解:

我们发现,这个“RootApproximant”出来,Tan[APO]是一个六次代数数,Tan[OP]也是一个六次代数数(如果换成Sin或Cos也一样,它们都是六次代数数),然后计算“与原值的差”:


这两个“与原值的差”都是小于$10^{-100}$的,注意本来WorkingPrecision就是100,所以现在已经非常有把握了,最后,我们使用RootReduce,代入原方程组进行检验:

我们发现,原方程组中的三个方程均满足,所以肯定是得到了精确解了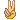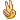
把方程组的代码贴一下,大家可以自己动手操作试试

1. θ = OP - 2 ArcTan[Csc[APO] (-Cos[APO] + Cos[APO] Cos[OP] + Sin[APO] Sin[OP])];
2. Solve[{1/2 (Cos[Pi - 2 APO + OP] + ((-1 + Cos[OP]) Cos[θ])/(-1 + Cos[θ])) == Cos[OP],
3.   1/2 (Sin[Pi - 2 APO + OP] + ((-1 + Cos[OP]) Sin[θ])/(-1 + Cos[θ])) == Sin[OP],
4.   2 (APO - ArcTan[(-1 + Cos[OP]) Cot[APO] + Sin[OP]]) == Pi - 2 APO + OP }, {APO, OP}]

Copy the Code

图中的精确解是

1. Tan[APO]->Root[-54 + 7 #1^2 + 3 #1^6 &, 2, 0],
2. Tan[OP]->Root[-648 + 5481 #^2 + 12954 #^4 + 6889 #^6& , 2, 0]

Copy the Code

TSC999

试了试，感觉不行。首先，近似值那么精确，是如何得到的？ 如果近似值选 1 和 0.3，能行不？

hbghlyj

回复 2# TSC999
近似值是用GeoGebra移动点$P$得到的
kuing.cjhb.site/forum.php?mod=viewthread& … 8&extra=page%3D1