|
|
Last edited by hbghlyj at 2024-6-8 20:11:00分段函数
\[f(x)=\sum_{n=1}^\infty\frac{\sin nx}n=\cases{0&若$x=2k\pi$\\\frac{1}{2} i \log (-e^{i x})&其它}\]
$\frac{1}{2} i \log (-e^{i x})=\pi\left\lceil\frac{x}{2 \pi}\right\rceil-\frac{x}{2}-\frac{\pi}{2}=-\pi\left\lfloor-\frac{x}{2 \pi}\right\rfloor-\frac{x}{2}-\frac{\pi}{2}$
周期$2π$跳跃间断点$2k\pi,k\inZ$
作为$\frac{\pi-x}2,x\in(0,\pi)$的Fourier $\sin$ series
$\sin(nx)$系数:$\frac2\pi\int_0^\pi\frac{\pi-x}2\sin(nx)\rmd x=\frac1n$
图像
\begin{tikzpicture}[domain=-4*pi:4*pi,x=.3cm]
\draw(0,pi/2)node[left]{$\frac\pi2$}--+(.4,0)(0,-pi/2)node[left]{$-\frac\pi2$}--+(.4,0);
\draw[->] (-14,0) -- (14,0) node[right] {$x$};
\draw[->] (0,-2) -- (0,2) node[above] {$f(x)$};
\foreach\a/\b in{-pi/-\pi,-2*pi/-2\pi,-3*pi/-3\pi,-4*pi/-4\pi,pi/\pi,2*pi/2\pi,3*pi/3\pi,4*pi/4\pi}{\draw(\a,0)node[below]{$\b$}--+(0,.15);}
\foreach\a in{-pi,-3*pi,pi,3*pi}\draw[red](\a+pi,-pi/2)--(\a-pi,pi/2);
\foreach\a in{-4*pi,-2*pi,0,2*pi,4*pi}\fill[red](\a,0)circle(1.5pt);
\end{tikzpicture}
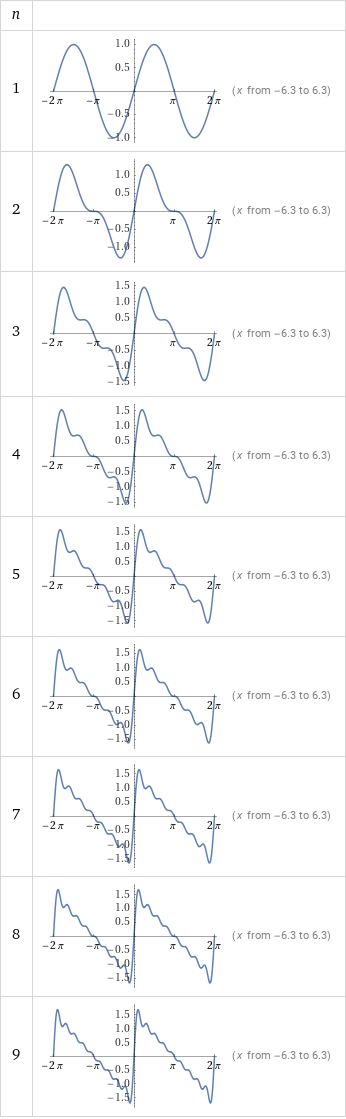
导函数$-\frac12+\pi\sum_{k\inZ}\delta(x-2k\pi)$
|
|