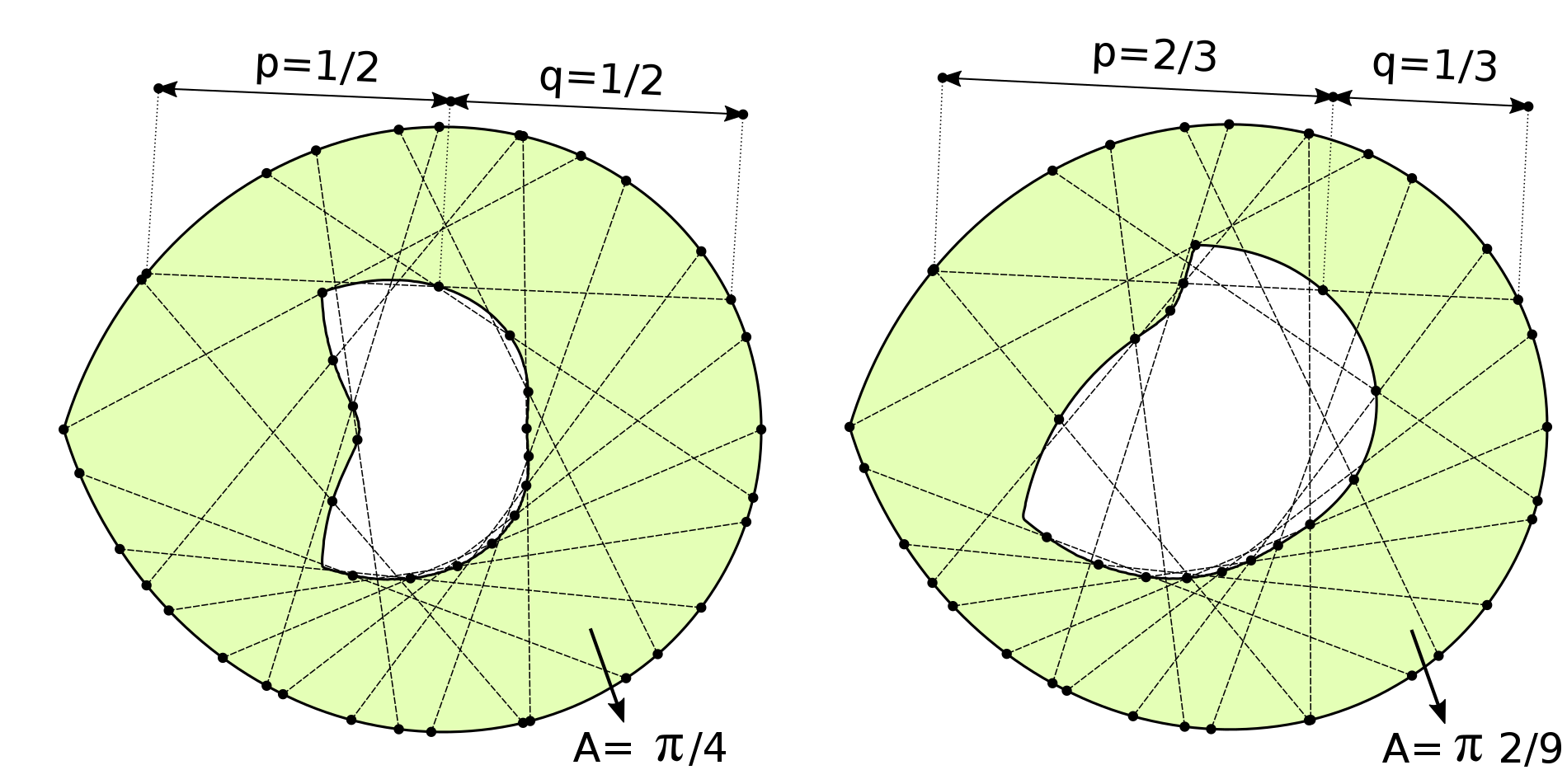
在凸闭合曲线内有固定长度的弦$AB$,弦上的一点$P$到$A$的距离为$c$,到$B$的距离为$c'$.
则$P$的轨迹是一条闭合曲线,它封闭的面积等于原始曲线的面积减 $π cc'$.
Wikipedia
GEOMETRICAL THEOREM. By Rev. Hamnet Holditch. The Quarterly Journal of Pure and Applied Mathematics, 2: 38
If a chord of a closed curve, of constant length $c+c^{\prime}$, be divided into two parts of lengths $c, c^{\prime}$ respectively, the difference between the areas of the closed curve, and of the locus of the dividing point, will be $\pi c c^{\prime}$.
SolutionLet $A B$ be the chord in any position; $P$ the dividing point, so that $A P=c, B P=c^{\prime}$; let $Q$ be the point in which the chord intersects its consecutive position; let $[A]$ be the area of the given curve, $[P],[Q]$, those of the loci of $P, Q$, respectively; $A Q=r, B Q=c+c^{\prime}-r$.
Then$$\tag1[A]-[Q]=\frac{1}{2} \int_0^{2 \pi} r^2 d \theta$$but also$$[A]-[Q]=\frac{1}{2} \int_0^{2 \pi} (c+c'-r)^2 d \theta$$therefore$$\frac{1}{2} \int_0^{2 \pi} r^2 d \theta=\frac{1}{2} \int_0^{2 \pi} (c+c'-r)^2 d \theta$$or$$\left(c+c^{\prime}\right) \int_0^{2 \pi} r d \theta=\frac{1}{2} \int_0^{2 \pi}\left(c+c^{\prime}\right)^2 d \theta$$therefore$$\int_0^{2\pi} r d \theta=\pi\left(c+c^{\prime}\right) \tag2$$
Also $[P]-[Q]=\frac{1}{2} \int_0^{2 \pi}(c-r)^2 d \theta$,
therefore, by (1), $\begin{aligned}[t]
[A]-[P]&=\frac{1}{2} \int_0^{2 \pi}\left(2 c r-c^2\right) d \theta\\&=c \int_0^{2 \pi} r d \theta-\pi c^2\\&=\pi c\left(c+c^{\prime}\right)-\pi c^2, \mathrm{by}(2)\\&=\pi c c^{\prime}\end{aligned}$ |