Maple calculator

hbghlyj

官网 在 AppStore / Google Play 均可下载. 手机上免费使用Maple的简单的功能.
以Legendre differential equation为例\begin{equation}\label1\left(  1-x^{2}\right)  y^{\prime\prime}-2xy^{\prime}+y=x^3
\qquad-1<x<1\end{equation}

有一个手写按钮	可以手写或拍照识别后，用软件的数学输入键盘修改	得到ODE的解

\eqref{1}没能给出分步解。对于简单的ODE可给出分步解:\begin{equation}\left(-xy'(x)\right)'=xy(x)\label2\end{equation}

hbghlyj

Mathematica 给出\eqref{1}的解太复杂了。由于右侧的forcing term $x^3$，Mathematica 似乎使其变得过于复杂。

1. ClearAll[y,x];
2. ode  = (1-x^2)y''[x]-2 x y'[x]+y[x]==x^3;
3. sol  = y[x]/.First@DSolve[ode,y[x],x]

Copy the Code

Maple 提供了形式更简单的解 (和1楼相同)

1. ode:= (1-x^2)*diff(y(x),x$2)-2*x*diff(y(x),x)+y(x)=x^3;
2. dsolve(ode,y(x));

Copy the Code

mathematica.stackexchange.com/questions/172659

hbghlyj

Mathematica 给出\eqref{2}的解

Maple手机版对\eqref{2}的解$y(x)=C_1\cos x+C_2\sin x$是错的
但是其Step-by-step solution给出的级数解$$y(x)=\sum_{k=0}^{\infty} a_{k} x^{k}, a_{k+2}=-\frac{a_{k}}{(k+2)^{2}}, a_{1}=0$$却是对的!

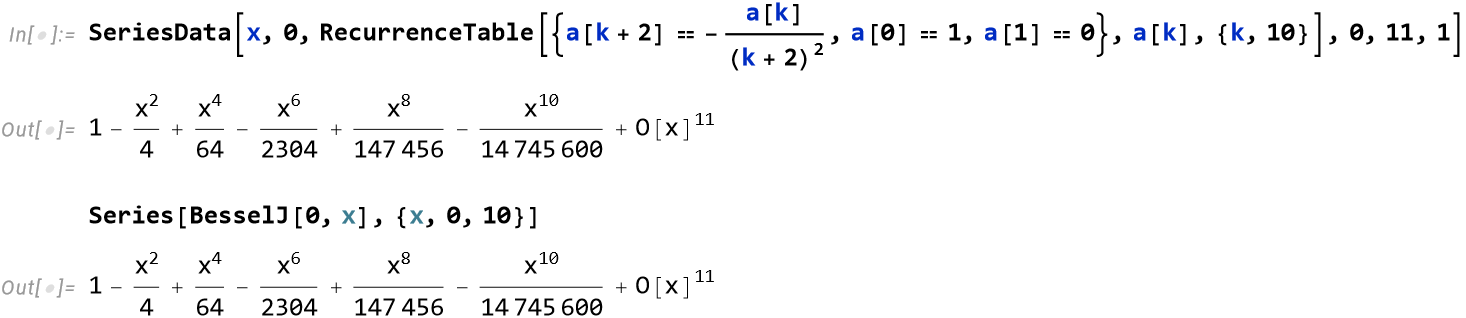
In[]:= SeriesData[x,0,RecurrenceTable[{a[k+2]==-(a[k]/(k+2)^2),a[0]==1,a[1]==0},a[k],{k,10}],0,11,1]

Out[]= 1-x^2/4+x^4/64-x^6/2304+x^8/147456-x^10/14745600+O[x]^11

In[]:= Series[BesselJ[0,x],{x,0,10}]

Out[]= 1-x^2/4+x^4/64-x^6/2304+x^8/147456-x^10/14745600+O[x]^11