等差数列、等比数列和等谐数列第$(a+2)$项构成几何级数

hbghlyj

Hall and Knight - Higher Algebra page 498:
93. An Arithmetic Progression, a Geometric Progression, and an Harmonic Progression have $a$ and $b$ for their first two terms shew that their $(n+2)$th terms will be in Geometric Progression if
$$\frac{b^{2 n+2}-a^{2 n+2}}{b a\left(b^{2 n}-a^{2 n}\right)}=\frac{n+1}{n}$$
一个等差数列、等比数列和等谐数列的前两个项都是$a$和$b$，那么它们的第$(n+2)$项构成等比数列，如果$$\frac{b^{2 n+2}-a^{2 n+2}}{b a\left(b^{2 n}-a^{2 n}\right)}=\frac{n+1}{n}$$

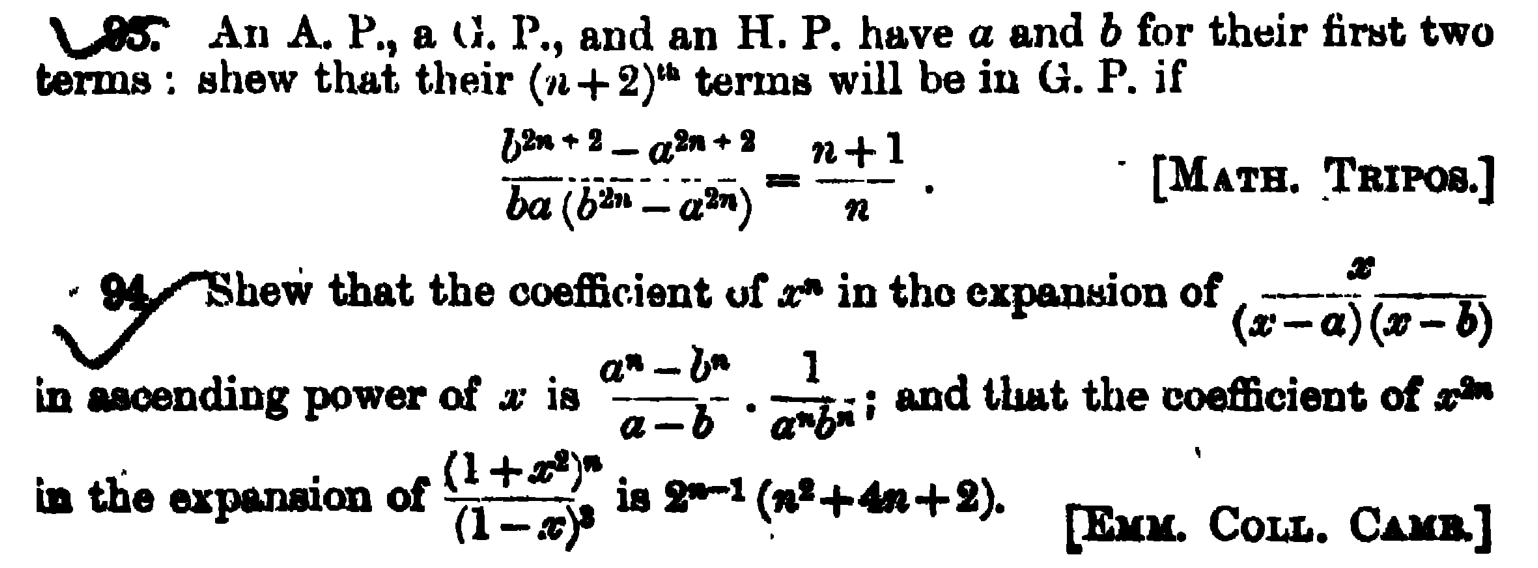
94. Shew that the coefficient of $x^n$ in the expansion of $\frac{x}{(x-a)(x-b)}$ in ascending power of $x$ is $\frac{a^n-b^n}{a-b} \cdot \frac{1}{a^n b^n} ;$ and that the coeffieient of $x^{2 n}$ in the expansion of $\frac{\left(1+x^2\right)^n}{(1-x)^3}$ is $2^{n-1}\left(n^2+4 n+2\right)$.
[Emmanuel College, Cambridge]

hbghlyj

$\left\{b+n (b-a),b \left(\frac{b}{a}\right)^n,\frac{1}{\frac{1}{b}+n \left(\frac{1}{b}-\frac{1}{a}\right)}\right\}$ are in G.P. $\Leftrightarrow\frac{b+n (b-a)}{\frac{1}{b}+n \left(\frac{1}{b}-\frac{1}{a}\right)}=\left(b \left(\frac{b}{a}\right)^n\right)^2\Leftrightarrow\left(\frac{b}{a}\right)^{2 n}=\frac{a (-a n+b n+b)}{b (a n+a-b n)}$
$$\frac{b^{2 n+2}-a^{2 n+2}}{b a \left(b^{2 n}-a^{2 n}\right)}=\frac{a}{b}\cdot\frac{\left(\frac{b}{a}\right)^{2 n} \left(\frac{b}{a}\right)^2-1}{\left(\frac{b}{a}\right)^{2 n}-1}=$$Plugging in $\left(\frac{b}{a}\right)^{2 n}=\frac{a (-a n+b n+b)}{b (a n+a-b n)}$
$$=\frac ab\cdot\frac{\frac{b (b-a n+b n)}{a (a+a n-b n)}-1}{\frac{a (b-a n+b n)}{b (a+a n-b n)}-1}=1+\frac{1}{n}$$

hbghlyj

$$\frac x{(x-a)(x-b)}=x\cdot\frac1{ab}\sum_{i=0}^\infty(\frac{x}a)^i\sum_{j=0}^\infty(\frac{x}b)^j$$
$x^n$系数$=\frac1{ab}\sum_{i=0}^{n-1}(\frac1a)^i(\frac1b)^{n-i-1}=\frac1{ab}\frac1{a^{n-1}b^{n-1}}\sum_{i=0}^{n-1}a^ib^{n-i-1}=\frac{a^n-b^n}{a-b}\cdot\frac1{a^nb^n}$
$$\frac{\left(1+x^2\right)^n}{(1-x)^3}=\sum_{i=0}^n\binom nix^{2i}\sum_{j=0}^\infty\binom{j+2}2x^j$$
$x^{2n}$系数$=\sum_{i=0}^n\binom ni\binom{2n-2i+2}2$

hbghlyj

最后还差证明$$\sum_{i=0}^n\binom ni\binom{2n-2i+2}2=2^{n-1}\left(n^2+4 n+2\right)$$即$$\sum_{i=0}^n\binom ni[4(n-i)(n-i-1)+10(n-i)+2]=2^n\left(n^2+4 n+2\right)\tag1$$
分别计算:
二次项:$$\sum_{i=0}^n\binom ni(n-i)(n-i-1)=\sum_{i=0}^{n-2}\binom ni(n-i)(n-i-1)=n(n-1)\sum_{i=0}^{n-2}{(n-2)!\over i!(n-i-2)!}=2^{n-2}n(n-1)$$
$$\implies\sum_{i=0}^n\binom ni4(n-i)(n-i-1)=2^n(n^2-n)$$
一次项:$$\sum_{i=0}^n\binom ni(n-i)=\sum_{i=0}^{n-1}\binom ni(n-i)=n\sum_{i=0}^{n-1}{(n-1)!\over i!(n-i-1)!}=n2^{n-1}$$
$$\implies\sum_{i=0}^n\binom ni10(n-i)=2^n(5n)$$
常数项:$$\sum_{i=0}^n\binom ni2=2^n(2)$$
相加得(1)式.

Related:
forum.php?mod=viewthread&tid=7224
forum.php?mod=viewthread&tid=2758