|
|
Last edited by hbghlyj 2024-3-8 09:15作业10 补充题五(选做):2)
在射影变换下,一条椭圆若映为一条双曲线,那么椭圆的内部映到了什么区域?
Example
射影变换$\left(
\begin{array}{cc|c}
1 & 0 & 0 \\
0 & 1 & 0 \\\hline
-1 & 1 & 1 \\
\end{array}
\right)$
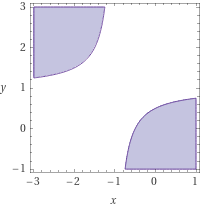
将圆内部$\{(x,y):x^2+y^2\le1\}$映射为$\left(\frac{x}{x-y+1}\right)^2+\left(\frac{y}{x-y+1}\right)^2\leq 1$
| 当$x>-1,y\le{2 x + 1\over2(x+1)}$; 当$x<-1,y\ge{2 x + 1\over2(x+1)}$. |
|
问题:有没有可能将圆内部映射到双曲线外部(两支之间的区域)?
相关帖子:forum.php?mod=viewthread&tid=10791 |
|