二元多项式是否在实数上可约

hbghlyj

这帖求出的
4x⁴ - 8x² y² - 9x² + 32x y² - 2x - 12y⁴ - 9y² + 3 = 0
WolframAlpha
看上去很像两条曲线的并集，它真的是一条不可约的曲线吗？

kuing

你已刷版，短暂禁言一天

hejoseph

这不是简单吗？不是看上去分成几段的曲线必定就是可约的，最简单的就是双曲线。

ellipse

在$\Bbb R[x,y]$不可约。

作一个二次扩域，在$\Bbb R[x,y,\sqrt{16 x^2 - 8 x + 25}]$上，就变可约了：

一个因式为
$24 y^2 = -8 x^2 - 4 (\sqrt{16 x^2 - 8 x + 25} - 8) x + 3 (\sqrt{16 x^2 - 8 x + 25} - 3)$

ellipse

上面利用了曲线的对称性解出$y^2$，但对一般的曲线（没有对称性），如果可以分成几个光滑的曲线分支，是否必在某个扩域上可分成这些分支呢？

“光滑的曲线分支”可以定义成“具有连续且光滑的参数化”。
例如双曲线$y^2-x^2=1$没有连续的参数化，但分成两个分支后，每个分支都有连续且光滑的参数化。这两个分支对应于在$\Bbb R[x,y,\sqrt{1+x^2}]$上分解的因式。

ellipse

举个例子 $(x^2 - 1)^2 + (y^2 - 1)^2-2 x^2 y^2=1.5$
有5个分支

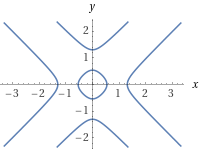
能否分解成5个因式，各对应1个分支：
WolframAlpha可以验证$2 x^2 y^2 + 1.5-(x^2 - 1)^2 - (y^2 - 1)^2=f_1f_2f_3f_4f_5$
$f_1=\frac{\sqrt{x^{2}+\frac{1}{8}}+\sqrt{y^{2}+\frac{1}{8}}-1}{\sqrt{x^{2}+\frac{1}{8}}+\sqrt{y^{2}+\frac{1}{8}}+1}$
$f_2=x-\sqrt{\left(1+\sqrt{y^{2}+\frac{1}{8}}\right)^{2}-\frac{1}{8}}$
$f_3=x+\sqrt{\left(1+\sqrt{y^{2}+\frac{1}{8}}\right)^{2}-\frac{1}{8}}$
$f_4=y-\sqrt{\left(1+\sqrt{x^{2}+\frac{1}{8}}\right)^{2}-\frac{1}{8}}$
$f_5=y+\sqrt{\left(1+\sqrt{x^{2}+\frac{1}{8}}\right)^{2}-\frac{1}{8}}$
曲线$f_1=0,f_2=0,f_3=0,f_4=0,f_5=0$各对应1个分支。
发到MSE问一问：math.stackexchange.com/questions/4861480