|
|
kuing
Posted 2024-6-25 15:06
第一题，如下图，设圆与 `y` 轴相切于 `H`，作 `PE\perp CD` 于 `E`，设 `CD` 与 `y` 轴及 `HP` 分别交于 `M`, `N`。
设 `P` 的纵坐标为 `y`，则 `y=\sqrt{r^2-(AB/2)^2}=\sqrt{3^2-5}=2`，即 `OH=2`，由于 `CD=AB`，所以也有 `PE=2`。
由于直线 `MN` 是 `y=\frac34x+b`，那么 `\Rtt NEP` 和 `\Rtt NHM` 都是三边比为 `3:4:5` 的三角形，由此可得 `PN=10/3`，则 `HN=19/3`，则 `HM=19/4`，则 `OM=11/4`，即 `b=-11/4`。
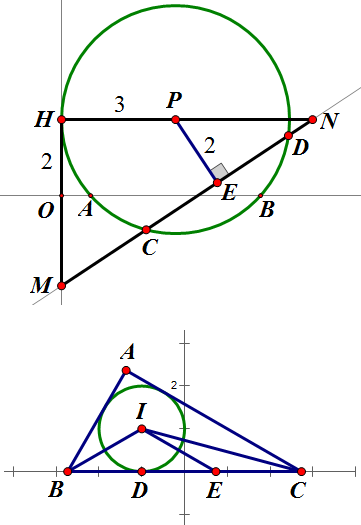
第二题，如上图，设内切圆与 `BC` 相切于 `D`，则由条件知 `BD=\sqrt3` 且 `CD=2+\sqrt3`，而 `ID=r=1`，所以 `IB=2` 且 `\angle IBD=30\du`，即 `\angle ABC=60\du`。
在 `CD` 上取一点 `E` 使 `IE=IB=2`，则 `DE=DB=\sqrt3`，则 `CE=2=IE`，于是 `\angle ECI=\angle EIC=\angle DEI/2=15\du`，从而 `\angle ACB=30\du`，所以 `\angle A=90\du`，则 `AB=r+BD=1+\sqrt3` 且 `AC=r+CD=3+\sqrt3`，所以面积 `S=\bigl(1+\sqrt3\bigr)\bigl(3+\sqrt3\bigr)/2`。 |
|
Ly-lie
Posted 2024-6-25 19:38
