cell-first projection of the 16-cell

hbghlyj

Cell-first Projection

The cell-first projection of the 16-cell has a cubical envelope. This projection is interesting in that all the edges of the 16-cell project onto the edges of the cube and the diagonals on the faces of the cube, forming a wireframe of the cube with each face crossed. It corresponds with the two possible ways to inscribe a tetrahedron inside a cube such that the edges of the tetrahedron lie on the faces of the cube.

The blue edges outline the cell closest to the viewer. Between this cell and the cubical envelope are 4 tetrahedral volumes that correspond with the 4 cells surrounding this blue cell. There are 6 cells that project onto the 6 faces of the cubical envelope (not shown here because they are being viewed edge-on). These 6 cells connect with the other side of the 16-cell, which contains the remaining 5 cells in a dual arrangement to the cells seen here. The following figure shows this opposite cell:

hbghlyj

1. Manipulate[ConvexHullMesh[Drop[RotationMatrix[{{1,1,1,1},{0,0,0,1}}].#[[1,1]],-1]&/@Table[RegionIntersection[Line[i],Hyperplane[{1,1,1,1},d]],{i,Tuples[{IdentityMatrix[4],-IdentityMatrix[4]}]}]],{d,-1,1}]

复制代码

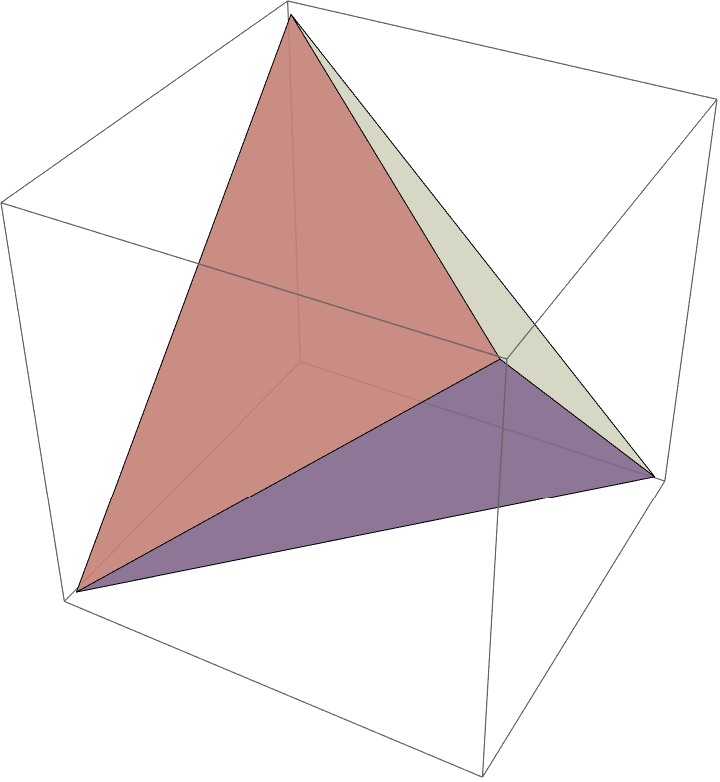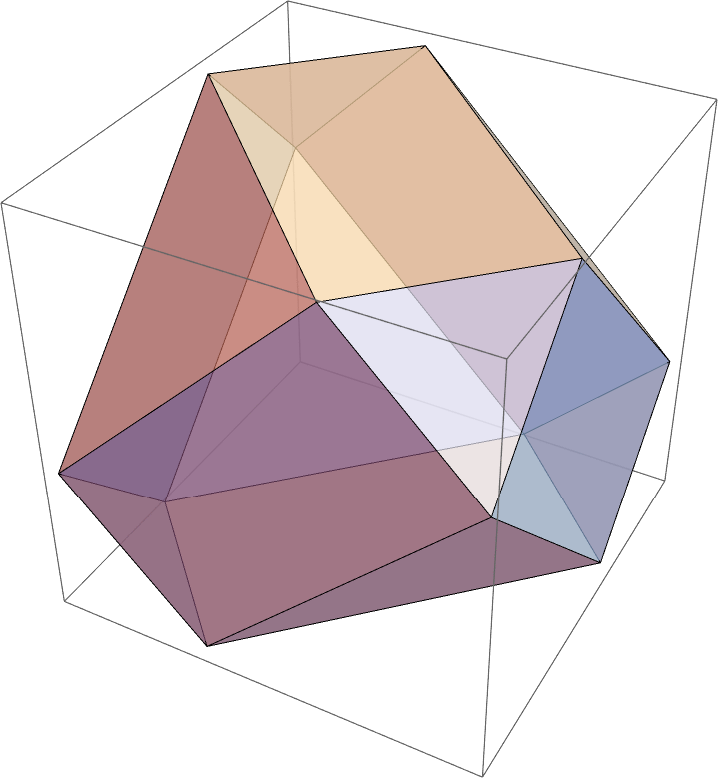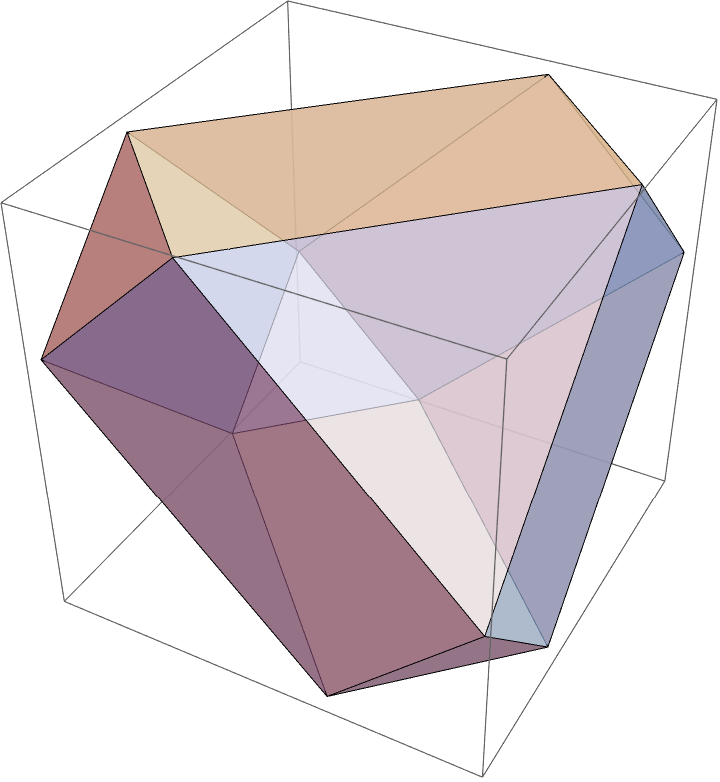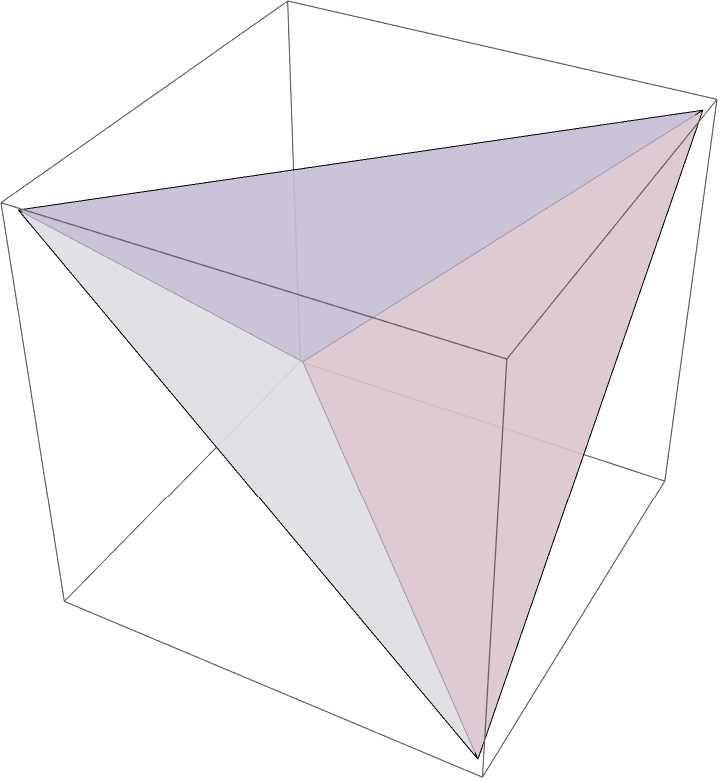
1. Export["anim.gif",Table[Graphics3D[{Opacity[.7],GraphicsComplex[{{0,0,t},{0,t,0},{t,0,0},{1-t,1,0},{1,1-t,0},{1,1,t},{1,0,1-t},{1-t,0,1},{1,t,1},{t,1,1},{0,1,1-t},{0,1-t,1}},Polygon[{{1,2,3},{4,5,6},{7,8,9},{10,11,12},{1,2,11,12},{1,3,7,8},{2,3,5,4},{5,6,9,7},{4,6,10,11},{8,9,10,12},{1,8,12},{2,4,11},{6,9,10},{3,5,7}}]]}],{t,0,1,0.05}],"DisplayDurations"->0.2]

复制代码

hbghlyj

如何对更复杂的四维多胞形（如 24 胞、120 胞、600 胞）进行相同的投影可视化？