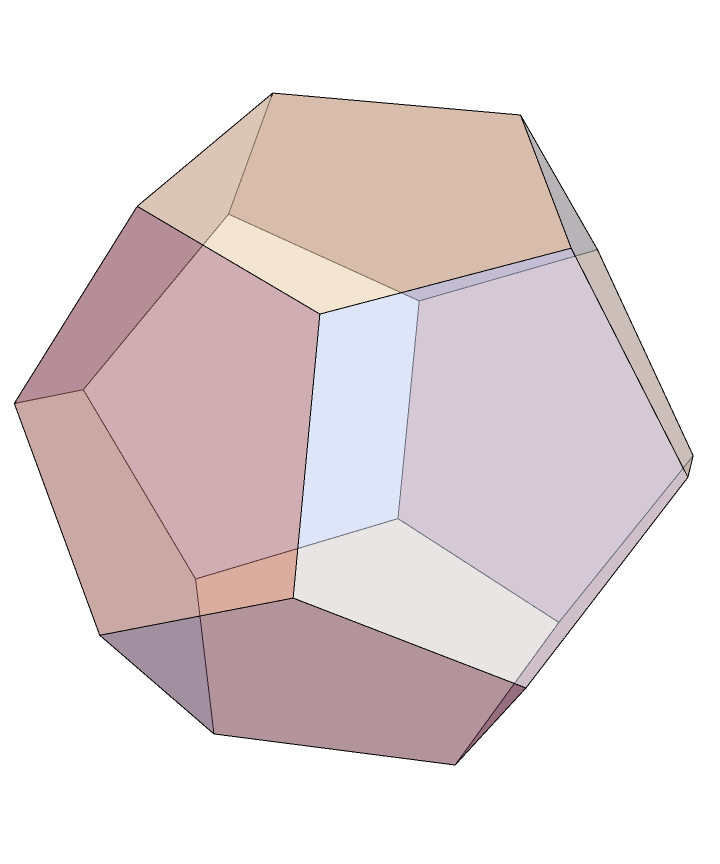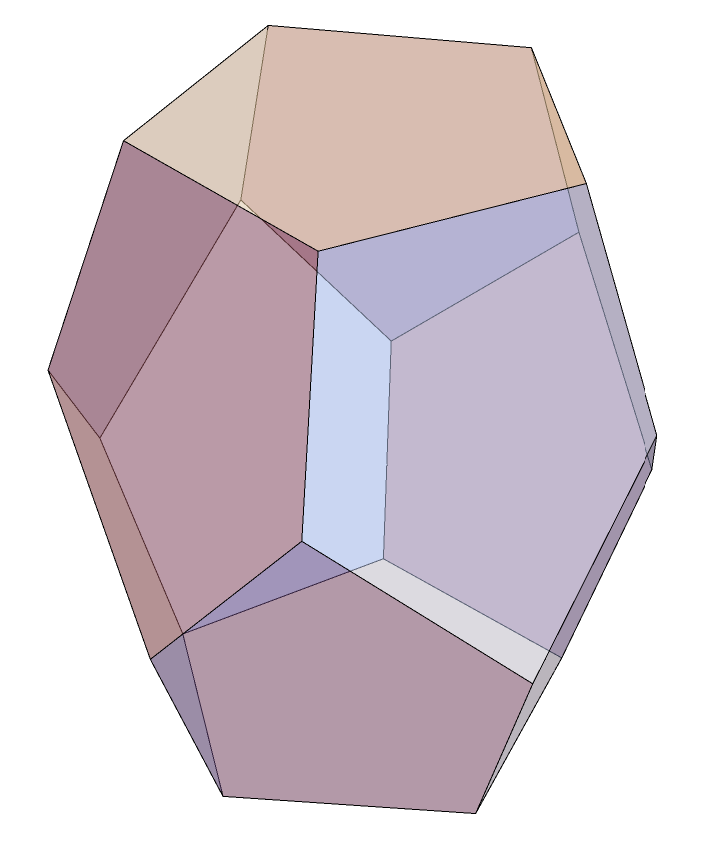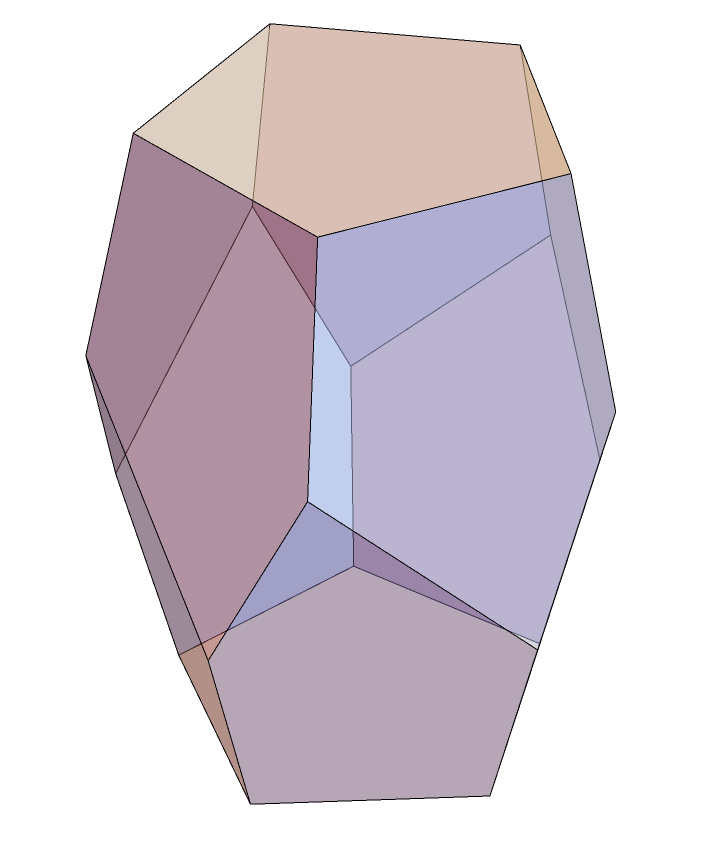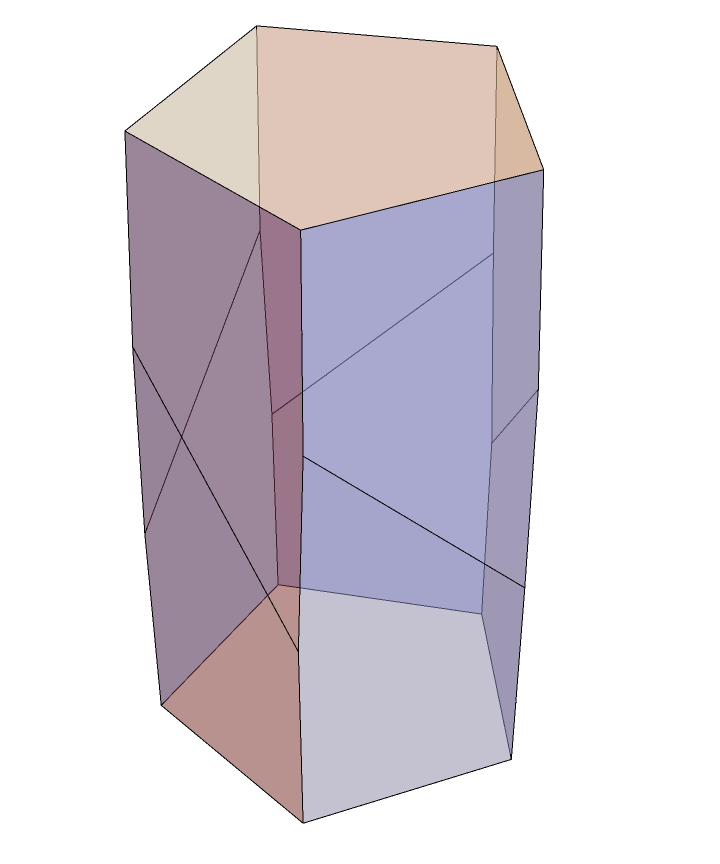
中间的斜的棱长设为 $x\in[1,\sqrt2]$,其余未变的棱长设为1,解不出精确表达式
- A1={r,0,z};
- A2=RotationTransform[2 Pi/5,{0,0,1}][A1];
- B1=RotationTransform[t,{0,0,1}][{r,0,-z}];
- B2=RotationTransform[2 Pi/5,{0,0,1}][B1];
- C1={1/(2 Sin[Pi/5]),0,Sqrt[1-(r-1/(2 Sin[Pi/5]))^2]+z};
- C2=RotationTransform[2 Pi/5,{0,0,1}][C1];
- D1=RotationTransform[t,{0,0,1}][{1/(2 Sin[Pi/5]),0,-Sqrt[1-(r-1/(2 Sin[Pi/5]))^2]-z}];
- {r0,t0,z0}={Cot[Pi/5],-\[Pi]/5,Sqrt[(5-Sqrt[5])/10]/2};
- Export["output.gif",Table[{r0,t0,z0}={r,t,z}/.FindRoot[{Total[(A1-B2)^2]-x^2,Total[(A1-B1)^2]-1,Det[{A1-B2,A2-B2,C1-A1}]},{{r,r0},{t,t0},{z,z0+MachinePrecision}}];
- Graphics3D[{Opacity[0.5],GraphicsComplex[{RotationTransform[2Pi/5,{0,0,1}][D1],RotationTransform[4 \[Pi]/5,{0,0,1}][C2],RotationTransform[2 \[Pi]/5,{0,0,1}][B2],B1,RotationTransform[2 \[Pi]/5,{0,0,1}][C2],RotationTransform[6 \[Pi]/5,{0,0,1}][C2],A2,A1,RotationTransform[6Pi/5,{0,0,1}][D1],RotationTransform[-2Pi/5,{0,0,1}][D1],C2,C1,RotationTransform[4 \[Pi]/5,{0,0,1}][A2],RotationTransform[4Pi/5,{0,0,1}][D1],D1,B2,RotationTransform[4 \[Pi]/5,{0,0,1}][B2],RotationTransform[6 \[Pi]/5,{0,0,1}][B2],RotationTransform[2 \[Pi]/5,{0,0,1}][A2],RotationTransform[6 \[Pi]/5,{0,0,1}][A2]}/.{r->r0,t->t0,z->z0},Polygon[{{15,10,9,14,1},{2,6,12,11,5},{5,11,7,3,19},{11,12,8,16,7},{12,6,20,4,8},{6,2,13,18,20},{2,5,19,17,13},{4,20,18,10,15},{18,13,17,9,10},{17,19,3,14,9},{3,7,16,1,14},{16,8,4,15,1}}]]},Boxed->False
- ],{x,1,Sqrt[2],(Sqrt[2]-1)/40}
- ],"DisplayDurations"->0.1]
|