D是△ABC的BC中点,延长AD交外接圆于E.延长CB交A点切线于P.在AE上取F点使DF=DE,证PA=PF

TSC999

D是△ABC的BC边中点，延长AD交外接圆于E。延长CB交A点切线于P。
在AE上取一点 F 使 DF=DE。证明 PA=PF

TSC999

先用不需要动脑子的复斜率几何方法证明此题：


为什么这种方法不需要动脑子？因为选定了某种构图方法以后，许多点的复数坐标公式事先都已算出，只须引用即可。
另一方面，直线与直线的交点坐标、点关于直线的各种镜像点、圆与直线的交点、直线线段的长度等等，也都有公式库可引用。
因而在多数情况下，用 mathematica 语言编写计算程序不会有多大困难。

TSC999

如何用钝几何方法做此题？

战巡

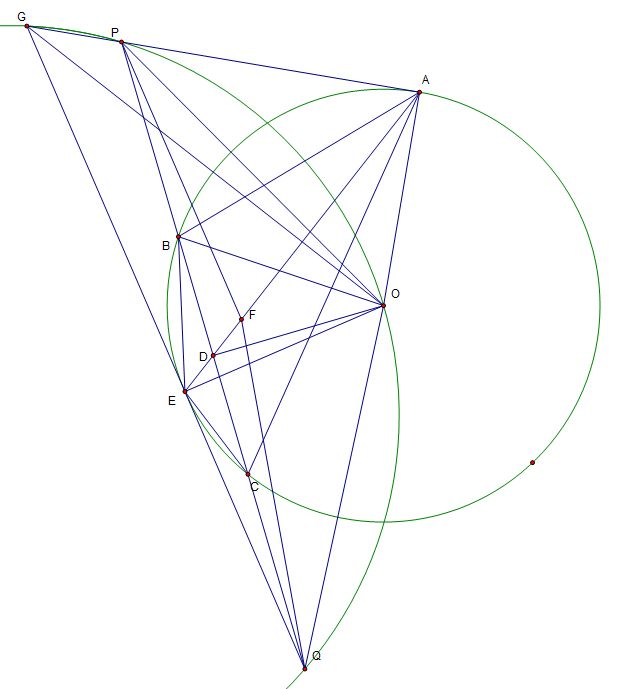
过$E$作圆切线，与直线$AP, BC$分别交于$G,Q$，其他连线如图

显然$OA\perp GP, OD\perp PQ, OE\perp GQ$，而且$A,D,E$共线，由西姆松逆定理，可知$G,P,O,Q$共圆。

另一方面，显然$\angle ODQ=\angle OEQ=90\du$，有$O,D,E,Q$共圆。
于是
\[\angle OQD=\angle OED=\angle EGO=\angle QPO\]
即有
\[OP=OQ\]
进而有
\[DP=DQ\]

而后，由梅涅劳斯定理，有
\[\frac{QE}{EG}\cdot\frac{GA}{AP}\cdot\frac{DP}{DQ}=1\]
注意我们知道$EG=GA$，故此
\[\frac{EQ}{AP}=\frac{DQ}{DP}=1\]
\[EQ=AP\]

又因为$DE=DF,DP=DQ$，$\angle PDF=\angle QDE$，有$\Delta PFD\cong\Delta DEQ$，即
\[EQ=PF\]
故此
\[AP=EQ=PF\]

TSC999

战巡 发表于 2025-4-2 14:55
过$E$作圆切线，与直线$AP, BC$分别交于$G,Q$，其他连线如图

显然$OA\perp GP, OD\perp PQ, OE\perp GQ$ ...

有一步没看懂：
∠OQD =∠OED 正确，因为都是 OD 弧上的圆周角。
∠EGO =∠QPO 正确，因为都是 OQ 弧上的圆周角。
为什么上面四个角都相等？即为什么 ∠OQD =∠OED=∠EGO =∠QPO 没看懂。

战巡

TSC999 发表于 2025-4-2 22:13
有一步没看懂：
∠OQD =∠OED 正确，因为都是 OD 弧上的圆周角。
∠EGO =∠QPO 正确，因为都是 OQ 弧上 ...

$GA,GE$都是切线，$EA\perp GO$，显然是有$\angle OEA=\angle EGO$的

TSC999

另一种证明如下，这个证明是【数学中国】网站的 数学小白新 网友做的。

作 DA 关于 OD 的对称线 DG ，则 $DA=DG, A G \px BC$ ，在 $E$ 点作圆 $O$ 的切线交 $B C$ 于 $Q$。以下证明 $\triangle D G Q$ 和 $\triangle D A P$ 关于直线 $O D$ 对称，故它们也全等：
显见 $\angle 1=\angle 2=\angle 3=\angle 8$ ，由于弦切角 $\angle 4=\angle 3$ ，而 $\angle 3=\angle 1$ ，故 $\angle 4=\angle 1$ ，因此 GDEQ 共圆，故 $\angle DEQ+\angle 5=180^{\circ}$ ，而 $\angle DEQ+\angle 6=180^{\circ}$ ，故 $\angle 5=\angle 6$ ，因 $\angle 6$ 和 $\angle 7$ 都是圆 O 中 AE 弦的弦切角，故 $\angle 6=\angle 7$ 。于是 $\angle 5=\angle 6=\angle 7$ 。在 $\triangle DGQ$ 和 $\triangle DAP$ 中， $DA=DG, \angle 8=\angle 1$ ， $\angle 7=\angle 5$ ，所以 $\triangle D G Q \cong \triangle D A P$ 。因此 $D Q=D P$ 且 $\triangle D G Q$ 和 $\triangle D A P$ 关于直线 $O D$ 对称。所以 $QC=PB, QB=PC$ ，故 $QE^2=QC \times QB=PB \times PC=PA^2$ ，于是 $QE=PA$ 。
又因为 $D$ 是 $P Q$ 的中点，也是 $E F$ 的中点，故 $P F Q E$ 是平行四边形，因此 $Q E=P F$ ，这样就最终推出 $P A=P F$ 。