来自人教群的一道二元不等式，其实只不过是……

kuing

题目：设 $x$, $y>0$，求证：
\[\frac{27}4(1+x^2)(1+y^2)\geqslant\bigl(x+y+\sqrt{1+x^2}+\sqrt{1+y^2}\bigr)^2\geqslant6\sqrt3(x+y).\]
看着看着突然由根号的形式想到几何意义，于是马上发现这题是怎么出的，下面就解壳。

如图所示。

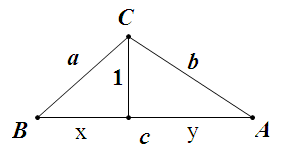
设 $\triangle ABC$ 面积为 $S$，由于 $c$ 边上的高为 $1$，则 $c=2S$。

先证左边，两边开方，由图知等价于
\[\frac{3\sqrt3}2ab\geqslant a+b+c,\]
由 $c=2S$ 知上式等价于
\[3\sqrt3abc\geqslant 4S(a+b+c),\]
由 $4S=abc/R$ 及 $a=2R\sin A$ 等可知上式等价于
\[\frac{3\sqrt3}2\geqslant \sin A+\sin B+\sin C,\]
这个大家都熟知了吧；

再证右边，两边平方，由图知等价于
\[(a+b+c)^4\geqslant 108c^2,\]
由 $c=2S$ 知上式等价于
\[(a+b+c)^4\geqslant 27\cdot 16S^2,\]
由海伦公式知 $16S^2=(a+b+c)(a+b-c)(b+c-a)(c+a-b)$，故上式等价于
\[(a+b+c)^3\geqslant 27(a+b-c)(b+c-a)(c+a-b),\]
由均值知显然成立。

综上，得证。

清楚这事儿后，就会觉得其实这题比较无聊……

isee

前半段联想太“狠”了

后半段亮出海伦公式基本就差不多了

虽然，偶还没看到怎么“均值”的

isee

前半段联想太“狠”了

后半段亮出海伦公式基本就差不多了

虽然，偶还没看到怎么“均值”的




还是 中等数学 的，不知道出题人是不是这个角度，怎么都感觉为出题而拼题……

kuing

前半段联想太“狠”了

后半段亮出海伦公式基本就差不多了

虽然，偶还没看到怎么“均值”的




还是 中等数学 的，不知道出题人是不是这个角度，怎么都感觉为出题而拼题……
isee 发表于 2013-12-10 00:27

右边三个括号均值一下就行了；
这题九成九就是这样出的，将两个简单的几何不等式通过等价变换和代换将形式搞复杂，再标准化变成二元，最后次数搞一搞，美化一下就出来了……

007

回复 3# isee


    $a+b+c=(a+b-c)+(b+c-a)c+a-b)\geqslant 3\sqrt[3]{(a+b-c)(b+c-a)(c+a-b)}$

007

回复 4# kuing


    为毛这些构造我想不到呢……

其妙

回复  kuing


    为毛这些构造我想不到呢……
007 发表于 2013-12-10 07:43

我也没想到，

其妙

不知道标答是怎样的？我也来试一试：
先证明右边不等式，（中午要休息）
由柯西不等式可得，$\sqrt {1+x^2}\geqslant\dfrac{x+\sqrt3}2$，

或者此式等价于$4(1+x^2)\geqslant(x+\sqrt3)^2$，展开后即$3x^2-2\sqrt3x+1\geqslant0$，此为显然；

于是$\bigl(x+y+\sqrt{1+x^2}+\sqrt{1+y^2}\bigr)^2
\geqslant\bigl(x+y+\dfrac{x+\sqrt3}2+\dfrac{y+\sqrt3}2\bigr)^2=\bigl[\dfrac32(x+y)+\sqrt3\bigr]^2\geqslant4\cdot\dfrac32(x+y)\cdot\sqrt3=6\sqrt3(x+y).
$
最后一步用了不等式$(m+n)^2\geqslant4mn.$