转发个问题，要求解析法

realnumber · 发表于 2013-8-30 17:55

一看到解析，不敢兴趣，哪位试下未命名.jpg

是解题群一老师问的“拒绝坐标法”，向量可以用，好奇怪的要求，难道是章节训练题.

其妙 · 发表于 2013-8-30 18:24

到底是要求解析法还是不准坐标法？

realnumber · 发表于 2013-8-30 19:03

后来透露出他坐标解决了，猜是别的都可以吧

kuing · 发表于 2013-8-30 19:19

解析法和坐标法有什么区别……

realnumber · 发表于 2013-8-30 19:28

原话复制的，估计他的坐标法指“设点的坐标”---瞎猜
我是连题目也懒得看，发贴原因是吸引人来论坛

kuing · 发表于 2013-8-30 20:27

既然说了向量可以用，那就用向量吧。
设 $CB=a$, $\vv{CB}=\vv a$, $CA=b$, $\vv{CA}=\vv b$，则
\begin{align*}
OG\perp CD&\iff\vv{CG}\cdot\bigl(\vv{CO}-\vv{CG}\bigr)=0 \\
& \iff\frac{\vv a+\vv b}3\cdot\Biggl( \vv{CO}-\frac{\vv a+\vv b}3 \Biggr)=0 \\
& \iff3\vv a\cdot\vv{CO}+3\vv b\cdot\vv{CO}=\bigl(\vv a+\vv b\bigr)^2 \\
& \iff\frac{3a^2}2+\frac{3b^2}2=a^2+b^2+2ab\cos C \\
& \iff\cos C=\frac{a^2+b^2}{4ab},
\end{align*}
……

kuing · 发表于 2013-8-30 22:06

用平几其实也很简单，如图
QQ截图20130830220338.png

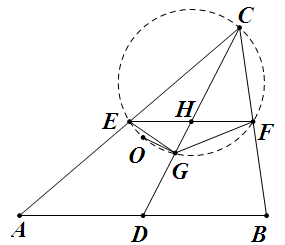
取 $CA$, $CB$ 的中点 $E$, $F$，由 $OG\perp CD$ 易知 $C$, $O$, $E$, $F$, $G$ 五点共圆。
设 $AB=c$，则 $EH=HF=c/4$, $CH=CD/2$, $HG=CG-CH=CD/6$，于是由相交弦定理及中线长公式得
\[\frac{c^2}{16}=EH\cdot HF=CH\cdot HG=\frac{CD^2}{12}=\frac{2a^2+2b^2-c^2}{48},\]
即得
\[c^2=\frac{a^2+b^2}2,\]
代余弦定理后亦得
\[\cos C=\frac{a^2+b^2}{4ab}.\]

kuing · 发表于 2013-8-30 22:10

咦？等一下，这样下去，取等的时候不就是等边三角形？但是题目不允许等边三角形，哼哼，这题有瑕疵……

其妙 · 发表于 2013-8-30 22:59

回复 8# kuing
改为求角C的取值范围就好了

		自动登录	找回密码
密码			快速注册

[几何] 转发个问题，要求解析法