人教论坛看到的一道几何证明选讲选做题

kuing

链接：bbs.pep.com.cn/forum.php?mod=viewthread&tid=2875165
题目：

1.（广东省汕头一中2013年高三4月模拟考试数学理试题）（几何证明选讲选做题）如图，$\odot O$ 的直径 $AB$ 的延长线与弦 $CD$ 的延长线相交于点 $P$，点 $E$ 是 $\odot O$ 上一点，$AE=AC$，$DE$ 交 $AB$ 于点 $F$，且 $AB=2BP=4$，则 $PF=\underline{\hspace{4em}}$

貌似不像平常那些几何证明选讲选做题那么简单耶，虽然一看就看出是 $P$ 和 $F$ 反演，但是常规的方法怎么证呢？

其妙

回复 1# kuing
反演？
是因为内外角平分线分线段成比例，构成的调和分割？

kuing

还是没看出什么简单方法，下面的解法可能严重复杂化。



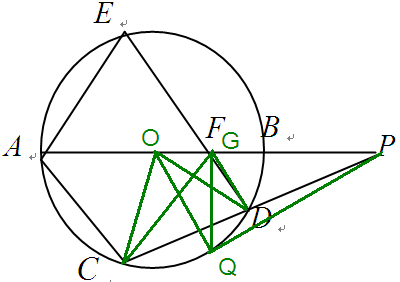
如图，过 $P$ 作 $\odot O$ 的切线，切点为 $Q$，过 $Q$ 作 $QG\perp AB$ 于 $G$，连结 $OC$、$OD$、$OQ$、$GC$、$GD$。
则 $PC\cdot PD=PQ^2=PO\cdot PG$，从而 $C$、$D$、$G$、$O$ 四点共圆，所以
\[\angle DGP=\angle OCD=\angle ODC=\angle CGA,\]
另一方面，由 $AE=AC$ 得
\[\angle DFP=\angle EFA=\angle CFA,\]
由此可见 $F$ 和 $G$ 重合，所以
\[PF=PG=\frac{PQ^2}{PO}=\frac{2PA\cdot PB}{PA+PB}=\frac{2\cdot6\cdot2}{6+2}=3.\]

第一章

第一章

反演神马的，看过，没记住，忘了……

其妙

回复 4# 第一章
这么快！

kuing

回复 4# 第一章

原来 AE=AC 是这样用的，果然是我严重复杂化了

kuing

还好没有给链接过去，不然糗大了

其妙

回复  kuing
反演？
是因为内外角平分线分线段成比例，构成的调和分割？
其妙 发表于 2013-9-3 23:15

还真的是反演与调和呢！

kuing

回复 9# 其妙

嗯，也不错

kuing

我之所以想得那么复杂，大概是因为我第一眼就将图形脑补成下面这样了

kuing

原贴那边 李斌755 的对称法很有型

其妙

回复 12# kuing
你那个切点弦的图就看出了极点和极线的关系，所以反演也成立，同时调和分割也成立
故$OP*OF=r^2=4$，$OP=4$，故$OF=1$，于是$PF=3$.

isee

哈哈，我当时见到这题，也想了一会，最后的解决方法就是第一章（共圆）与其妙（角分线比例性质）的方法均想出

说反演的话就不太常规了，还不如说根轴实在点




还准备发论坛玩玩的，不过，当时没几个会员，也觉得这题与高考的方向不太一致，就没发了

其妙

回复 14# isee
反演和两圆的根轴是有关系的，学会了用【/cy】