|
|
链接：bbs.pep.com.cn/forum.php?mod=viewthread&tid=2878327
发贴ID：liaoweiyi888
点P是直线2x+y=4上一点，PA，PB是圆x^2+y^2=1的两条切线，切点为A ,B，求三角形PAB面积的最小值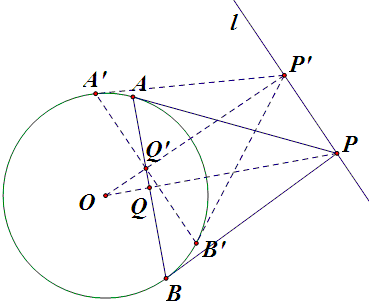
设 $\odot O$ 的半径为 $R$，连结 $OP$ 交 $AB$ 于 $Q$，过 $O$ 作 $OP'\perp l$ 于 $P'$，过 $P'$ 作 $\odot O$ 的两条切线，切点分别为 $A'$, $B'$，连结 $A'B'$ 交 $OP'$ 于 $Q'$，如图所示。
因为 $OQ\cdot OP=R^2=OQ'\cdot OP'$，所以 $P$, $P'$, $Q'$, $Q$ 四点共圆，而 $\angle Q'P'P=90\du$，故 $\angle Q'QP=90\du$，由此可见，$AB$ 恒过点 $Q'$。
所以 $AB\geqslant A'B'$，又显然有 $PQ\geqslant P'Q'$，故
\[S_{\triangle PAB}=\frac12AB\cdot PQ\geqslant \frac12A'B'\cdot P'Q'=S_{\triangle P'A'B'},\]
当且仅当 $P$ 与 $P'$ 重合时取等。 |
|
hongxian
发表于 2013-9-16 15:57
