|
|
Author |
isee
Posted 2014-6-22 22:44
Last edited by isee 2014-6-22 23:08以上来自沈文选的平面几何证明方法全书，第30页。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
随后，有“所谓”（绝没有贬意，也不褒）的简明证明，如——（来自网络，原作者不详，可能是 梁卷明）
证明(就是楼上证法2的提示的具体构造之一)：
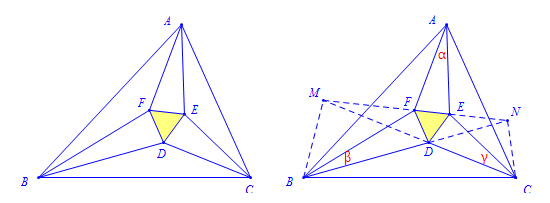
如图左，设$\triangle ABC$中$\angle A=3\alpha$，$\angle B=3\beta$，$\angle C=3\gamma$。
构造如图右的图形：
使得$\triangle AFE$中，$\angle EAF=\alpha$，$\angle AFE=60^\circ＋\beta$，则$\angle AEF=60^\circ＋\gamma$；
以$EF$为边向$\triangle AFE$外作等边$\triangle DEF$；
类似$\triangle AEF$的构造过程，
分别以$DF$、$DE$为边向$\triangle DEF$外分别构造$\triangle BDF$、$\triangle DCE$。
延长$BD$、$CD$，与直线$EF$分别交于$M$、$N$，连结$AB$、$BC$、$CA$、$MB$、$NC$。
$\therefore \triangle MDE$中，$\angle EMD=\angle EDC-\angle DEM=\beta$，
$\therefore B$、$D$、$F$、$M$四点共圆，$\angle MBD=\angle EFD=60^\circ$。
同理可证，$C$、$D$、$E$、$N$四点共圆， $\angle NCD=\angle FED=60^\circ$，
$\therefore \angle MBN=\angle NCM\Rightarrow B、C、N、M$四点共圆，
$\therefore \angle DBC=\angle NBC=\angle NMC=\beta,\angle DCB=\angle MCB=\angle MNB=\gamma$，
同理可证，$\angle ECA=\gamma$，$\angle EAC=\alpha$，$\angle FAB=\alpha$，$\angle FBA=\beta$，
与图左对照，可知图1中$\triangle DEF$是正三角形。 |
|
kuing
Posted 2014-4-27 22:14
其妙
Posted 2014-6-22 23:34
青青子衿
Posted 2014-6-23 11:10
你完全可以的嘛
