来自人教群的$AG\perp BG$求值

kuing

渝X教师多多(2859*****)  17:11:29

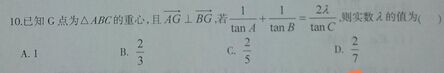
如何处理？

题目：已知 $G$ 点为 $\triangle ABC$ 的重心，且 $\vv{AG}\perp\vv{BG}$，若 $1/\tan A+1/\tan B=2\lambda/\tan C$，则实数 $\lambda$ 的值为[选项略]

\begin{align*}
0&=3\vv{AG}\cdot3\vv{BG} \\
& =\bigl(\vv{AB}+\vv{AC}\bigr)\cdot\bigl(\vv{BA}+\vv{BC}\bigr) \\
& =-\vv{AB}^2+\vv{AB}\cdot\bigl(\vv{BC}-\vv{AC}\bigr)+\vv{AC}\cdot\vv{BC} \\
& =-2AB^2+\frac{AC^2+BC^2-\bigl(\vv{AC}-\vv{BC}\bigr)^2}2 \\
& =\frac{a^2+b^2-5c^2}2,
\end{align*}
得到
\[a^2+b^2=5c^2,\]
故
\begin{align*}
\lambda &=\frac{\tan C}2\left( \frac1{\tan A}+\frac1{\tan B} \right) \\
& =\frac{\sin C}{2\cos C}\cdot \frac{\cos A\sin B+\cos B\sin A}{\sin A\sin B} \\
& =\frac{\sin ^2C}{2\cos C\sin A\sin B} \\
& =\frac{c^2}{2ab\cos C} \\
& =\frac{c^2}{a^2+b^2-c^2} \\
& =\frac14.
\end{align*}

kuing

这个贴的题有点类似 forum.php?mod=viewthread&tid=159

kuing

差点忘了记录群里后来聊天记录中的解法。

鄂L教师yuzi(5755*****) 18:08:31

kuing

刚才提问人又再一次在群里问……唉，不过还好，这次群里还给了出处。

津A教师Mike(3061*****)  16:30:32

过程其实跟我的一样，不过省略了一些计算过程

其妙

这里好像也有？blog.sina.com.cn/s/blog_54df069f0101epje.html

yhg1970

差点忘了记录群里后来聊天记录中的解法。
kuing 发表于 2015-1-18 16:34

     还可以用解析法，设A(-1,0)，B(1,0)，G(cosθ,sinθ)，则C(3cosθ,3sinθ)，用斜率公式和到角公式表示tanA、tanB、tanC，运算稍微麻烦些。

isee

回复 5# 其妙

果然题还是要自己写才会有更特别的感觉。。。。今天碰到了。。。

其妙

回复  其妙

果然题还是要自己写才会有更特别的感觉。。。。今天碰到了。。。 ...
isee 发表于 2019-1-27 12:56

四年前的帖子了，你又翻出来，
看了下博客里发表的时间是2013-08-26 18:54:17