来自人教群的等腰三角形面积最大值

kuing

川R教师临疯(3579*****)  15:18:41


粤A爱好者kuing(249533164)  15:27:47
不正确

粤A爱好者战巡(3705*****)  15:32:49
阿波罗尼斯圆啊
粤A爱好者战巡(3705*****)  15:36:39

这个等价于求S△ABD最大值，显然A点在B、D和k所确定的阿氏圆上，取最值显然就在这个圆的顶点
算出来好像是l^2/(2(1-k^2))吧

川R爱好者临疯(3579*****)  16:15:12
谢谢，弄明白了。

话说用海伦的话似乎更方便计算最终结果。

题目：在等腰 $\triangle ABC$ 中，$AB=AC$，$D$ 在线段 $AC$ 上，$AD=kAC$（$k$ 为常数，且 $0<k<1$），$BD=l$ 为定长，则 $\triangle ABC$ 的面积最大值为？

解：设 $AB=AC=x$，则 $AD=kx$，由海伦公式及均值得
\begin{align*}
\S{ABC}&=\frac1k\S{ABD} \\
& =\frac1{4k}\sqrt{(l+x+kx)(x+kx-l)(kx+l-x)(l+x-kx)} \\
& =\frac{1-k^2}{4k}\sqrt{\left( x^2-\frac{l^2}{(1+k)^2} \right)\left( \frac{l^2}{(1-k)^2}-x^2 \right)} \\
& \leqslant \frac{1-k^2}{8k}\left( \frac{l^2}{(1-k)^2}-\frac{l^2}{(1+k)^2} \right) \\
& =\frac{l^2}{2(1-k^2)},
\end{align*}
取等略。

isee

逆命题：forum.php?mod=viewthread&tid=3813

再见到是知乎提问的，有了新想法.


题：在 $\triangle ABC$ 中 $a=4,\sin C=2\sin B$，则 $\triangle ABC$ 的面积最大值为______.

Solution 1
求最值，在不知道什么是阿波罗尼斯圆的前提下，不等式最快.

（注意到恒等式 $a^2-b^2>0$，$c^2-d^2>0$ 时

\begin{align*} \color{blue}{(a^2-b^2)(c^2-d^2)}&=(ac-bd)^2-(ad-bc)^2\\[1em] &\color{blue}{\leqslant (ac-bd)^2}-0, \end{align*}

即有 $\color{blue}{(a^2-b^2)(c^2-d^2)\leqslant (ac-bd)^2}$，当且仅当 $a/c=b/d$ 等号成立.）




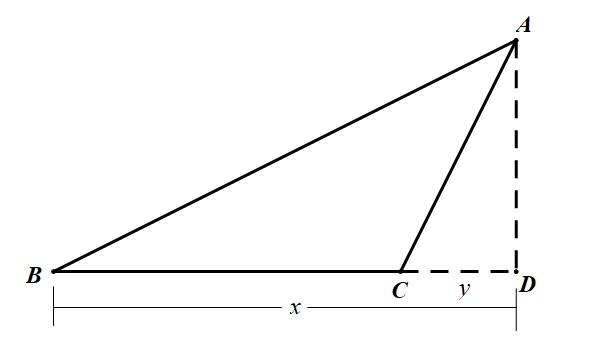
图1 AD 垂直于 BC


如图 1，由条件易知 $c^2=4b^2$. 记点 $A$ 作 $BC$ 上的投影为 $D.$ 即 $BD,CD$ 为有向线段.

记 $BD=x,$ $CD=y$ 则 $x-y=4,$ $x^2+AD^2=c^2$， $y^2+AD^2=b^2.$

条件化为 $x^2+AD^2=4(y^2+AD^2)$ 即 $3AD^2=x^2-4y^2$ 从而

\begin{align*} 3AD^2=\frac 43\cdot \color{blue}{\left(1-\frac 14\right)(x^2-4y^2)}&\leqslant \frac 43\color{blue}{(x-y)^2}\\[1em] \Rightarrow AD&\leqslant \sqrt {\frac 43\cdot 4^2\cdot \frac 13}=\frac 83. \end{align*}

所以 $S_{\triangle ABC}=\frac 12 \cdot a\cdot AD\leqslant \frac {16}3.$

等号时， $\frac 1x=\frac {1/2}{2y}$ 即 $BD=\frac {16}3$，$CD=\frac 43$.

Solution 2

无法接受此法，则可用海伦-秦九韶公式（这第四次用了，刚刚的第三次）

$\begin{align*} S&=\frac 12\sqrt {a^2b^2-\left(\frac {a^2+b^2-c^2}2\right)^2}\\[1em] &=\frac 12\sqrt {16b^2-\left(\frac {16+b^2-4b^2}2\right)^2}\\[1em] &=\frac 12\sqrt {-\frac 94b^4+16b^2-64}\\[1em] \end{align*}$

这显然是关于 $b^2$ 的二次函数，下略.