一道几何题

king12123

isee

与2015年湖北理科第14题好像啊。

forum.php?mod=viewthread&tid=3525

色k

N点多余？

abababa

回复 1# king12123

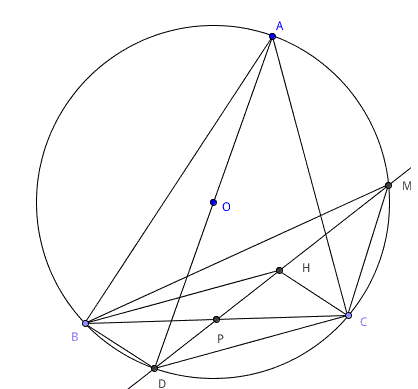
设$AD$是$\odot O$的直径，则$BD\perp AB$，又因为$CH\perp AB$，所以$BD\sslash CH$，同理$CD\sslash BH$，所以四边形$BDCH$是平行四边形
设$DH$交$BC$于$P'$，则$P'$是$BC$的中点，与$P$重合，所以$D,P,H,M$四点共线
因为$\frac{BM\cdot PM\cdot\sin\angle DMB}{2}=S_{\triangle BMP}=S_{\triangle CMP}=\frac{PM\cdot CM\cdot\sin\angle DMC}{2}$，所以$\frac{BM}{CM}=\frac{\sin\angle DMC}{\sin\angle DMB}=\frac{CD/2R}{BD/2R}=\frac{CD}{BD}=\frac{BH}{CH}$

king12123

楼上证明太精彩了。

isee

回复  king12123

设$AD$是$\odot O$的直径，则$BD\perp AB$，又因为$CH\perp AB$，所以$BD\sslash CH$， ...
abababa 发表于 2015-8-27 19:59

完全不同高考，原来是竞赛题，用到了顶点到垂心的距离是外心到对边距离的2倍……

abababa

回复 6# isee
其实没用到那个结论，只是辅助线的添加方法是一样的。
4楼最后那步如果改成$BM\cdot BD\cdot\sin\angle DBM=2S_{\triangle BDM}=2S_{\triangle CDM}=CM\cdot CD\cdot\sin\angle DCM$，因为$\angle DBM+\angle DCM=180^\circ$，正弦值相等，所以$BM\cdot BD=CM\cdot CD$，显得更简单一点