|
|
抛物线 维基有一个GIF图：
File:Parabola construction given five points.gif
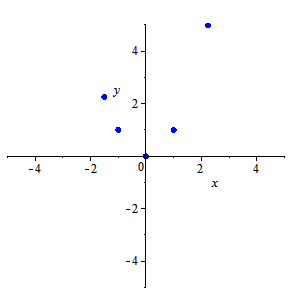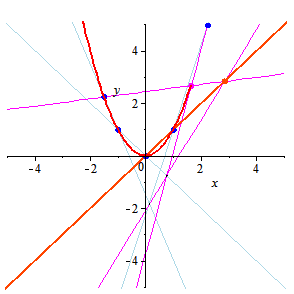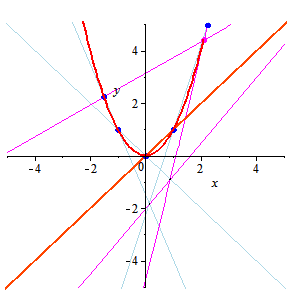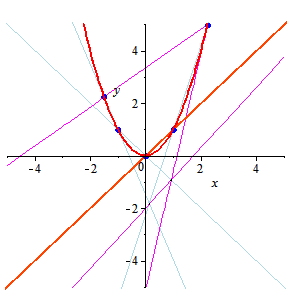Two parabolas, intersecting in four points may be distinct. But if they intersect in five points, then they coincide, so a parabola, like ellipse and hyperbola, is defined by five points. Here, we construct parabola, given five points. For the description of the method see p. 83 of the following book: A.P. Veselov, E.V.Troitsky. Lectures in Analytical Geometry. 2nd ed., in Russian. Lan', 2003. See also a description and an applet for the ellipse here.
|
|
hbghlyj
发表于 2024-3-27 08:08
