关于四面体的表面积体积两个问题

realnumber

沈阳李明(875----35) 2017-01-08 17:15:57
1.我提的未解问题是，已知三棱锥的三个侧面顶角分别为α,β,γ，且底面面积为定值S，求三棱锥的最大体积Vmax.
（沈阳李明(87－－－835)  18:53:01
【百元征解题】对第一位破解我提出问题者，我将给予100元红包打赏！该问题发表于全国不等式研究会会刊《不等式研究通讯》2011年第1期。注:三个顶角都相等的情形我已解决，最大体积是正三棱锥。一般的情形尚未解决！沈阳李明 2017年1月8日.）



宁波邵剑波(953------3) 2017-01-08 17:19:29
2．表面积一定的四面体中,以正四面体的体积最大，这也不好证明

realnumber

２＇体积固定的四面体中，以正四面体的表面积最小，这个可以这样证明，好像和１楼的问题２等价，说明见３楼．

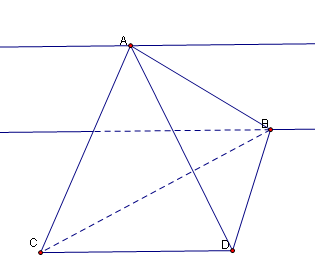
如图，分别过A,B作CD的平行线，当A,B分别在平行线上移动时，四面体ABCD体积不变，且，其中两侧面ACD,BCD面积也不变．
　　当AB垂直CD，AB最短，若再有AC=AD且BC=BD，则C,D到AB的距离和最小（可以建立空间直角坐标系证明的，CD为x轴，CD,AB公垂线段长度m所在直线为Z轴，C(-a,0,0),D(a,0,0),两平行线所确定的面上动点为P(x,y,m),容易证明CP+DP最小时，y=0,x=0且此时CP,DP正好垂直AB），即三角形CAB,三角形DAB的面积和最小．配合反证法，当四面体不是正四面体时，总找得到表面积更小的等体积四面体．因此可以证明２＇．

realnumber

由２＇成立，得出２成立，可以这样证明：
表面积为S的四面体中，体积最大的四面体为ABVD,体积为V,假设它不是正四面体，那么
那么由２＇可以得到等体积的正四面体EFGH，其表面积小于S,记为S'.把EFGH按比例放大使得表面积变为S,那么体积比四面体ABCD更大，这与开始部分的结论矛盾．所以假设错误，即ABCD应该为正四面体．即２成立．

kuing

回复 3# realnumber

那第一个问题是否也等价于：底面上的高为定值H，求底面面积S的最小值？

realnumber

回复 4# kuing
应该是的，推理一样．
百度到一个可能会用到的公式
已知任意四面体P-ABC，记$PA=a，PB=b，PC=c，\cos{∠APB}=x，\cos{∠BPC}=y，\cos{∠CPA}=z$，则：$V_{PABC}=\frac{1}{6}abc\sqrt{1+2xyz-x^2-y^2-z^2}$－－－－bioweapon
来自tieba.baidu.com/p/2588543174

hejoseph

第一问不用找简单的答案了，肯定没简单结论的，这相当于求 $PA\cdot PB\cdot PC$ 的最大值，若令 $\cos\angle BPC=7/8$，$\cos\angle CPA=3/4$，$\cos\angle APB=5/4$，$S_{\triangle ABC}=1/4$，则 $PA\cdot PB\cdot PC$ 的最大值是方程
\[
48168083344329x^{16}-416889933899400x^{12}+26040537828864x^8-255515959296x^4+293601280=0
\]
的一个正根，约为
\[
1.7120806159837147764
\]

realnumber

恩，晓得了

kuing

又是高次方程……立体真是比平面复杂得多，想起之前这题：forum.php?mod=viewthread&tid=151 这么简单的条件结果都是高次方程……

kuing

不过，虽然最大值没有简单结果，但我们还可以尝试寻找取最大值时的四面体有什么特征。

hejoseph

暂时没看出有什么简单的特征来