|
|
教学乡长 13:42:41
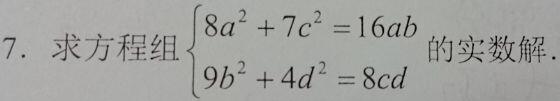
啥子个思路
$\xcancel{解法一}$ 由均值 $8a^2+7c^2=16ab\leqslant 8a^2+8b^2\riff 7c^2\leqslant 8b^2$, $9b^2+4d^2=8cd\leqslant 4c^2+4d^2\riff 9b^2\leqslant 4c^2$,从而 $\frac78c^2\leqslant b^2\leqslant \frac49c^2\riff b=c=0\riff a=d=0$。
$\xcancel{解法二}$ 两式相加配方得 $b^2+3c^2+8(a-b)^2+4(c-d)^2=0\riff a=b=c=d=0$。
注:这两个解法的本质明显相同,所以没必要写“解法一”“解法二”,应视为同一解法。 |
|