请问：有没有抛物线光学性质的平几证法？

lemondian

请那位提供一下，谢谢！

kuing

当然有，简单问题麻烦自己思考，不要做伸手党。

lemondian

这个证明，行不？

其妙

当然有，简单问题麻烦自己思考，不要做伸手党。
kuing 发表于 2018-4-11 16:36

郭老师教训的极是，有老师的派头了，（众所周知的，比好多老师都厉害）

lemondian

这个呢？

游客

回复 5# lemondian


    抛物线的光学性质是什么？这个过程的倒数第二行的叙述在逻辑上很混乱。

lemondian

回复 6# 游客
抛物线的光学性质：
从抛物线的焦点处发出的光线照射到抛物线上，经抛物线反射后，反射光线平行于抛物线的轴。
*********************
一边找资料，一边学着写过程，别见笑   
有好想法，请多指点，谢谢！

游客

回复 7# lemondian


    那要先作垂线，再证角相等，最后说明那是反射光线。
入射角等于反射角不是证明出来的，那是光学原理。

lemondian

回复 8# 游客


    感 谢！

zhcosin

这个问题要自己想出来才算有意思，看别人的答案没啥意义。

其妙

回复  lemondian


    抛物线的光学性质是什么？这个过程的倒数第二行的叙述在逻辑上很混乱。 ...
游客 发表于 2018-4-12 13:58

感觉也是逻辑混乱，虽然证明的“点”找到了些

hbghlyj

ESA Senior Years - Senior Topic 2a - The reflection property of the parabola

Let \(P(2ap,ap^2)\) be a point on the parabola \(x^2=4ay\) with focus at \(S\) and let \(T\) be the point where the tangent at \(P\) cuts the \(y\)-axis. Suppose \(PQ\) is a ray parallel to the \(y\)-axis. Our aim is to show that the line \(PS\) will satisfy the reflection property, that is, \(\angle QPB\) is equal to \(\angle SPT\). Notice that, since \(QP\) is parallel to \(ST\), \(\angle QPB\) is equal to \(\angle STP\), so we will show that \(\angle STP = \angle SPT\). Now \(S\) has coordinates \((0,a)\), and \(T\) has coordinates \((0,-ap^2)\), obtained by putting \(x=0\) in the equation of the tangent at \(P\). Hence\[ SP^2=(2ap-0)^2+(ap^2-a)^2 = a^2(p^2+1)^2 \] after a little algebra. Also, \[ ST^2 = (a+ap^2)^2= a^2(1+p^2)^2 \]and so \(SP=ST\). Hence \(\Delta STP\) is isosceles and so \(\angle STP = \angle SPT\).

A Proof of the Reflective Property of the Parabola, Robert C. Williams, The American Mathematical Monthly, Vol. 94, No. 7 (Aug. - Sep., 1987), pp. 667-668

An important property of parabolas is the following: a ray of light emanating from the focus of a parabolic mirror is always reflected along a line parallel to the axis of the parabola. This fact is equivalent to the statement that the lines through the focus $F$ and an arbitrary point $P$ on the parabola and through $P$ parallel to the axis of the parabola make equal angles $\alpha$ and $\beta$ with the line tangent to the curve at $P$.

All of the calculus books that I know prove (or direct the student property by proving that $\tan\alpha=\tan\beta$ via a cumbersome trigonometric analysis. Here is a short proof that, although it uses a little calculus, is more geometric. This proof is not new (see, for instance, [1, pp. 94-95]), but it certainly seems not to be well known. Reference [1] C. Smith, An Elementary Treatise on Conic Sections, Macmillan, London, 1885. OpenMathDep | Internet Archive

In the figure, we have the parabola with equation $y=x^{2} / 4 c$, with focus $F(0, c)$ and directrix $y=-c . P\left(x_{0}, y_{0}\right)$ is a point on the parabola, $l_{1}$ is the line through $P$ and parallel to the axis of the parabola, and $l_{2}$ is the line through $P$ and tangent to the parabola. $D\left(x_{0},-c\right)$ is the intersection of $l_{1}$ with the directrix and $E$ is the intersection of $l_{2}$ with the line $F D$. Line $l_{2}$ has slope $x_{0} / 2 c$ (using calculus) while $F D$ has slope $-2 c / x_{0}$, so that these are perpendicular. Since $|\overrightarrow{F P}|=|\overrightarrow{P D}|$, the right triangles $F E P$ and $D E P$ are congruent. Thus $\beta=\angle F P E=\angle D P E=\alpha$. It is also easy to verify that the point $E$ lies on the $x$-axis.

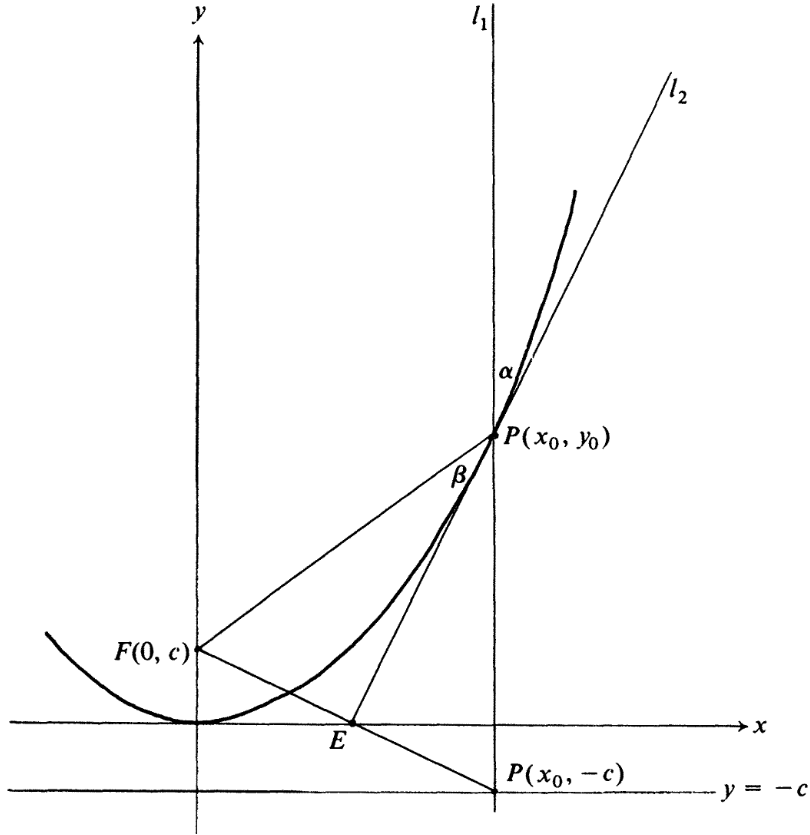
这个图把$D$错标成了$P$.

Reflective Property

Begin with a line (the directrix), and a point labeled $F$. Select an arbitrary point $A$, on the directrix, and construct a segment from that point to the focus (segment $AF$). Now we know that any point on the perpendicular bisector of segment $AF$ is equidistant from the end points. Thus we now construct the perpendicular bisector of segment $AF$. The point on the parabola must be on this bisector. We also know that the distance of a point to a line, is the perpendicular segment from the point to the line. Therefore we construct line $j$ through the point $A$ perpendicular to the directrix $d$. The point where $j$ intersect $k$, is the required point on the parabola.

Theorem: The tangent line at a point $P$ on a parabola makes equal angle with the line through $P$ parallel to the axis of symmetry and the line through $P$ and the focus.

Line $EP$ is tangent to the parabola at $P$. The point $P$ is a point on the parabola, and $P$ is equidistant from $F$ and $D$ (by definition). Therefore segment $PE$ is the altitude of isosceles triangle $PFD$, and angle $FPE$ is congruent to angle $EPD$. Since vertical angles are congruent, angle $EPD$ is congruent to angle $CPA$.

Classroom Capsules - A Proof of the Reflective Property of the Parabola, Howard Sporn
The College Mathematics Journal, Volume 53, 2022 - Issue 1
Pages 67-68 | Received 12 Jul 2019, Accepted 01 Sep 2020, Published online: 15 Nov 2021

We may state the theorem as follows. See Figure 1. We draw the parabola having focus $F$ and directrix $d$. We call its vertex $V$. We choose any point $P$ on the parabola other than $V$. We draw the tangent line $t$ to the parabola at $P$. We define the angle $∠1$ to be the acute angle formed by $FP$ and $t$, and with $V$ in the interior. Then we draw the ray $r$ with endpoint $P$ pointing away from $d$. We define $∠2$ to be the acute angle formed by $r$ and $t$. We wish to prove that $∠1≅∠2$.	Fig. 1 A parabola with focus $F$ and directrix $d$, showing a tangent $t$ to the parabola at $P$ and the angles $∠1$ and $∠2$.
Now, remove the tangent line $t$ for the moment. We let $Q$ be the foot of the perpendicular from $P$ to $d$. See Figure 2. We let $M$ be the midpoint of $\overline{FQ}$, and let $S$ be the reflection of $P$ in $M$. Therefore, $MF = MQ$ and $MP = MS$. So, by side-angle-side, $ΔFMP≅ΔQMS$, and therefore $FP = QS$. By a similar argument, $PQ = SF$. Now, since the distance from a point on a parabola to the focus is equal to the distance from the point to the directrix, we have $FP = PQ$. Therefore, quadrilateral $FPQS$ is a rhombus.	Fig. 2 The parabola with the constructed rhombus.
We now need to show that line $\overleftrightarrow{MP}$ is indeed the tangent line $t$. Let $X$ be any point on that line other than $P$. Since the diagonals of a rhombus are perpendicular, line $\overleftrightarrow{MP}$ is the perpendicular bisector of $\overline{FQ}$. If $X$ is not the point $M$, then by side-angle-side, $ΔFMX≅ΔQMX$, and therefore, $FX = XQ$. If $X$ is the point $M$, then obviously we still have $FX = XQ$. Now drop a perpendicular from $X$ to the directrix $d$. Call the foot of that perpendicular $Y$. If $X$ is not on $d$, $ΔXYQ$ is a right triangle with hypotenuse $QX$. Therefore, $XY < QX$, and so $XY ≠ FX$. Therefore, $X$ cannot lie on the parabola. If, on the other hand, $X$ lies on the directrix $d$, then $X$ and $Y$ are the same point, and so $XY = 0 ≠ FX$, and again $X$ cannot lie on the parabola.	$P$ is the only point on $\overleftrightarrow{MP}$ that lies on the parabola, and so $\overleftrightarrow{MP}$ is the tangent line $t$. We now define $∠1$ and $∠2$ as before. The line segment $\overline{PS}$ is a diagonal of the rhombus. Therefore, $∠1≅∠MPQ$. The angles $∠MPQ$ and $∠2$ are vertical angles and thus congruent. Therefore $∠1≅∠2$, which completes the proof.

这里“切线”是与抛物线只有1个公共点且不平行于对称轴的直线.(同样的,圆锥曲线的切线与光学性质总结帖)