|
|
 游客
游客
posted 2018-6-11 13:56
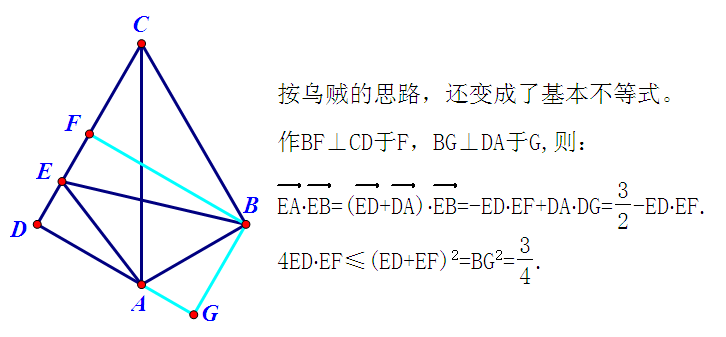
Last edited by hbghlyj 2025-4-6 21:47按乌贼的思路,还变成了基本不等式。
作 $\mathrm{BF} \perp \mathrm{CD}$ 于 $\mathrm{F}, \mathrm{BG} \perp \mathrm{DA}$ 于 G ,则:
\[
\begin{aligned}
& \overrightarrow{\mathrm{EA}} \cdot \overrightarrow{\mathrm{~EB}}=(\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{DA}}) \cdot \overrightarrow{\mathrm{EB}}=-\mathrm{ED} \cdot \mathrm{EF}+\mathrm{DA} \cdot \mathrm{DG}=\frac{3}{2}-\mathrm{ED} \cdot \mathrm{EF} . \\
& 4 \mathrm{ED} \cdot \mathrm{EF} \leqslant(\mathrm{ED}+\mathrm{EF})^2=\mathrm{BG}^2=\frac{3}{4}
\end{aligned}
\]
2楼的运算可以用上这个矩形。 |
|