与角的两边相切的圆的半径

player1703

已知$\angle$BAC内一点D:
a)求作$\odot$O使得$\odot$O过点D且与AB, AC都相切.
b)若$\angle$BAC=$\alpha$, 点D到AB,AC的距离分别为$d_1$,$d_2$. 求$\odot$O的半径.

part a) 尺规作图我自己想出来了. 作D关于角平分线的对称点就转化成这个问题了:
forum.php?mod=viewthread&tid=5478&extra=page=1

part b) 如果$\angle$BAC是直角, 建立直角坐标系用圆的方程可以解出$r=d_1+d_2\pm\sqrt{2d_1d_2}$. 不是直角怎么办?

kuing

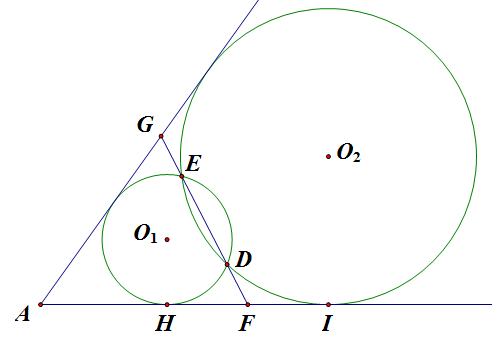
如图，则有
\begin{align*}
DF&=d_1\sec\frac\alpha2,\\
DG&=d_2\sec\frac\alpha2,\\
FG&=DF+DG=(d_1+d_2)\sec\frac\alpha2,\\
AF&=\frac{FG}2\csc\frac\alpha2=\frac{d_1+d_2}2\sec\frac\alpha2\csc\frac\alpha2,\\
FH&=FI=\sqrt{FD\cdot FE}=\sqrt{FD\cdot DG}=\sqrt{d_1d_2}\sec\frac\alpha2,\\
AH&=AF-FH=\left( \frac{d_1+d_2}2\csc\frac\alpha2-\sqrt{d_1d_2} \right)\sec\frac\alpha2,\\
AI&=AF+FI=\left( \frac{d_1+d_2}2\csc\frac\alpha2+\sqrt{d_1d_2} \right)\sec\frac\alpha2,\\
r_1&=AH\tan\frac\alpha2=\left( \frac{d_1+d_2}2-\sqrt{d_1d_2}\sin\frac\alpha2 \right)\sec^2\frac\alpha2,\\
r_2&=AI\tan\frac\alpha2=\left( \frac{d_1+d_2}2+\sqrt{d_1d_2}\sin\frac\alpha2 \right)\sec^2\frac\alpha2.
\end{align*}
当 $\alpha=90\du$ 时和你算的一样，应该没错。

player1703

回复 2# kuing 谢谢! 我用几何画板验证了结果是对的