一道对角线垂直的圆内接四边形证线段相等题目

郝酒

圆的内接四边形ABCD，AC⊥BD，I是三角形ABD的内心，IE⊥BD于E，IA=IC，求证：IE=CE.

被困扰了许久，导角吧，最后归结为证角ACD=角BCE，要证CEO共线；直接导比例吧，最后归结为要证DC+CB=2R，或者sin角DAC+sin角BAC=1.
都卡住了，愿大侠出手：）

kuing

感觉在哪见过，等 isee, 乌贼等出手了……

郝酒

双向延长DE交圆于P，Q，由OI是AC的中垂线，可得OI垂直PQ，所以I是PQ中点。
延长DI，BI交圆于G，F.可知GF垂直平分AI,设GF交PQ于L，由蝴蝶定理得IE=IL，进而梯形ACEL是等腰梯形，所以AL=IL=IE=CE.

isee

回复 2# kuing


显然竞赛题，我啃不动，3#的解答直接用了蝴蝶定理，的确是感觉在哪儿见过~

kuing

回复 4# isee

这个证法的确很帅，有点难想，我还是想想不用辅助线的三角法好了……

kuing

再次使用 forum.php?mod=viewthread&tid=5513 中的三角方法。

下面将 `\triangle ABD` 的三个角 `\angle DAB`, `\angle ABD`, `\angle ADB` 简记为 `A`, `B`, `D`。



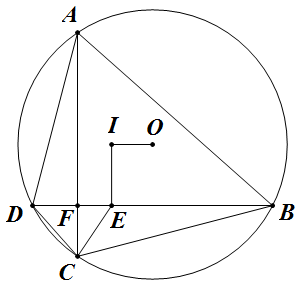
由 `IA=IC` 知 $OI\px BD$，所以
\[r=R\cos A, \quad(*)\]
则
\[\cos A=\frac rR=4\sin\frac A2\sin\frac B2\sin\frac D2=2\sin\frac A2\left( \cos\frac{B-D}2-\sin\frac A2 \right),\]
化简得
\[2\sin\frac A2\cos\frac{B-D}2=1. \quad(**)\]

根据欧拉公式 `OI^2=R^2-2Rr` 得
\[OE=\sqrt{OI^2+r^2}=R-r,\]
可见要证 `IE=CE`，只需证 `C`, `E`, `O` 三点共线，即证 `\cos\angle ACO=\cos\angle IEO`，即证
\[\frac{AC}{2R}=\frac r{R-r},\]
由式 (*), (**) 得
\[\frac r{R-r}=\frac{\cos A}{1-\cos A}=\frac1{2\sin^2\frac A2}-1=2\cos^2\frac{B-D}2-1=\cos(B-D),\]
所以等价于证明
\[AC=2R\cos(B-D).\]

设 `AC` 与 `BD` 交于 `F`，则在 `\triangle ABD` 中有
\[AF=AD\sin D=2R\sin B\sin D,\]
同理在 `\triangle CBD` 中有
\[CF=2R\cos B\cos D,\]
两式相加即得 `AC=2R\cos(B-D)`，即得证。

kuing

和那帖一样，此证明可能走了弯路，因为式 (**) 也等价于 `\cos B+\cos D=1`，很可能有巧妙方法瞬间得出来。

Tesla35

tieba.baidu.com/p/5831191120

tieba.baidu.com/p/3897982776

tieba.baidu.com/p/1786393568

tieba.baidu.com/p/1245007834

tieba.baidu.com/p/5794943775

色k

回复 8# Tesla35

贴吧dang

Tesla35

这TM都是啥啊。

kuing

回复 10# Tesla35