|
|
Last edited by hbghlyj 2023-7-5 01:29Apollonius, Thale's theorem and Orthic triangle by 杨圣汇
| Michael Penn 在他在 YouTube 上的户外讲座系列中发布了这个问题,这是一个更普遍的几何问题的一部分,称为Apollonius问题:仅使用直尺和圆规找到与三个给定圆相切的圆。 |
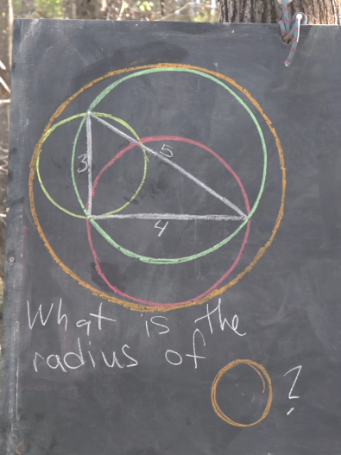
| | 您还可以查看 Mathmaniac的视频 关于使用 circle inversion 解决一些一般情况,对于分离的基圆。 |
|
我要展示一个代码,这段代码解决了Michael的问题对于任意三角形。拖动一个顶点可即时求解。
这里的Apollonius函数使用内切圆的定义。两个内切圆之间的距离等于它们的半径差。重复定义 3 次,将所有内容包装在FindRoot函数中。- Apollonius[c1_,c2_,c3_,r1_,r2_,r3_]:=With[{gc=(c1+c2+c3)/3},\[IndentingNewLine]FindRoot[{\[IndentingNewLine]EuclideanDistance[{x,y},c1]\[Equal]r-r1,\[IndentingNewLine]EuclideanDistance[{x,y},c2]\[Equal]r-r2,\[IndentingNewLine]EuclideanDistance[{x,y},c3]\[Equal]r-r3\[IndentingNewLine]},{{x,gc[[1]]},{y,gc[[2]]},{r,r1+r2+r3}}]]
FindRoot需要初值。所以我仔细选择了给定的三个圆心的重心作为第四个圆心的初值。这保证了求解的收敛性。选择半径之和作为第四个半径的初始值的原因相同。
按照Michael的问题的陈述,将给定三角形的三边作为直径即可。使用Manipulate创建动画,不失一般性将三角形的两个点定在原点和 {2,0}。- a={0,0};\[IndentingNewLine]b={2,0};\[IndentingNewLine]Manipulate[\[IndentingNewLine]c1=Midpoint[{a,b}];\[IndentingNewLine]c2=Midpoint[{b,c}];\[IndentingNewLine]c3=Midpoint[{c,a}];\[IndentingNewLine]r1=EuclideanDistance[a,b]/2;\[IndentingNewLine]r2=EuclideanDistance[b,c]/2;\[IndentingNewLine]r3=EuclideanDistance[c,a]/2;\[IndentingNewLine]Graphics[{\[IndentingNewLine]{Transparent,EdgeForm[{Thick,Red}],Triangle[{a,b,c}]},\[IndentingNewLine]{Dashed,Circle[c1,r1],Circle[c2,r2],Circle[c3,r3]},\[IndentingNewLine]{Red,Circle[{x,y},r]/.Apollonius[c1,c2,c3,r1,r2,r3]}\[IndentingNewLine]}],\[IndentingNewLine]{{c,{3,4}/2},Locator,Appearance-> None},SaveDefinitions->True\[IndentingNewLine]]
|
|