求证三个角的正切之积为1

hbghlyj

If $A+B+C=\pi$ and $\cos A=\cos \theta \sin \phi$, $\cos B=\cos \phi \sin \Psi$, $\cos C=\cos \Psi \sin \theta$, then find the value of $\tan \theta \tan \phi \tan \Psi$.

---

几何意义是: 直三面角O-ABC, $A=\angle BAC,B=\angle ABC, C=\angle ACB$,
$\theta=\angle OAC,\phi=\angle OBA,\Psi=\angle OCB$.
由三面角余弦定理, $\cos A=\cos \theta \sin \phi$, $\cos B=\cos \phi \sin \Psi$, $\cos C=\cos \Psi \sin \theta$.
而 $\tan \theta \tan \phi \tan \Psi=\frac{OB}{OA}\frac{OC}{OB}\frac{OA}{OC}=1$.

Wikipedia–Trigonometry of a tetrahedron
Trihedral Angle
Elementary Geometry

色k

盲目地随性地推了一通居然就推了出来，希望没有问题。

设 `x_1=\cos\theta`, `y_1=\sin\theta`, `x_2=\cos\phi`, `y_2=\sin\phi`, `x_3=\cos\Psi`, `y_3=\sin\Psi`，则 `x_i^2+y_i^2=1`, `i=1`, `2`, `3`，设 `f=\tan\theta\tan\phi\tan\Psi`，即 `f=y_1y_2y_3/(x_1x_2x_3)`。

由 `A+B+C=\pi` 得 `\cos^2A+\cos^2B+\cos^2C+2\cos A\cos B\cos C=1`，代入条件即
\[(x_1y_2)^2+(x_2y_3)^2+(x_3y_1)^2+2x_1x_2x_3y_1y_2y_3=1,\]
消 `y` 得
\[x_1^2(1-x_2^2)+x_2^2(1-x_3^2)+x_3^2(1-x_1^2)+2(x_1x_2x_3)^2f=1,\]
整理得
\begin{align*}
2(x_1x_2x_3)^2f
&=1-x_1^2-x_2^2-x_3^2+x_1^2x_2^2+x_2^2x_3^2+x_3^2x_1^2\\
&=(1-x_1^2)(1-x_2^2)(1-x_3^2)+(x_1x_2x_3)^2\\
&=(y_1y_2y_3)^2+(x_1x_2x_3)^2\\
&=(x_1x_2x_3)^2f^2+(x_1x_2x_3)^2,
\end{align*}
从而
\[2f=f^2+1,\]
即 `f=1`。

isee

回复 1# hbghlyj

建议楼主看一看置顶公式输入，更方便交流。只是建议。

hbghlyj

$A+B+C=\pi$,\begin{align*}
\cos A&=\cos\alpha_{1,2}\cos\alpha_{1,3}-\sin\alpha_{1,2}\sin\alpha_{1,3}\frac{\cos (\alpha_{3,1}+\alpha_{2,1})+\cos(\alpha_{1,2}+\alpha_{3,2})\cos(\alpha_{1,3}+\alpha_{2,3})}{\sin(\alpha_{1,2}+\alpha_{3,2})\sin(\alpha_{1,3}+\alpha_{2,3})}\\
\cos B&=\cos\alpha_{2,3}\cos\alpha_{2,1}-\sin\alpha_{2,3}\sin\alpha_{2,1}\frac{\cos (\alpha_{1,2}+\alpha_{3,2})+\cos(\alpha_{2,3}+\alpha_{1,3})\cos(\alpha_{2,1}+\alpha_{3,1})}{\sin(\alpha_{2,3}+\alpha_{1,3})\sin(\alpha_{2,1}+\alpha_{3,1})}\\
\cos C&=\cos\alpha_{3,1}\cos\alpha_{3,2}-\sin\alpha_{3,1}\sin\alpha_{3,2}\frac{\cos (\alpha_{2,3}+\alpha_{1,3})+\cos(\alpha_{3,1}+\alpha_{2,1})\cos(\alpha_{3,2}+\alpha_{1,2})}{\sin(\alpha_{3,1}+\alpha_{2,1})\sin(\alpha_{3,2}+\alpha_{1,2})}\end{align*}则\[\sin\alpha_{2,1}\sin\alpha_{3,2}\sin\alpha_{1,3}=\sin\alpha_{1,2}\sin\alpha_{2,3}\sin\alpha_{3,1}\]

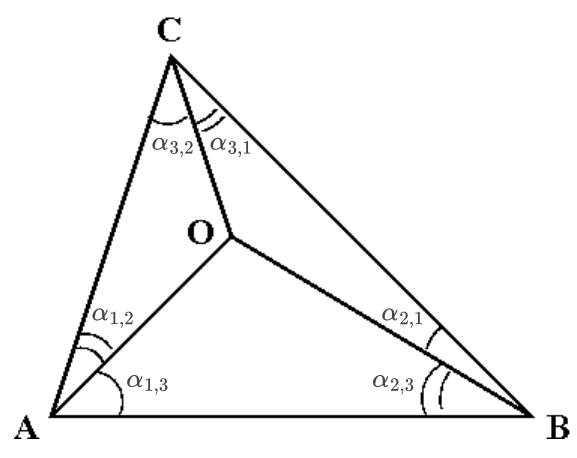
几何意义:$A,B,C$和$\alpha_{i,j}$是四面体的面角