请大师们看看向量这个怪兽

走走看看

1010jiajiao.com/gzsx/shiti_id_9bcdc2401573137dcd725ddeabf379c5
如图所示，当OC⊥AB时，向量|a−b|最小。
似乎是这回事，但理由是什么呢？

而在如下链接中却采用解析的方式，似乎又太过费事。
zhidao.baidu.com/question/545115877.html

kuing

设 `O` 到 `AB` 的距离为 `h`，则 `AB=2\sqrt{1-h^2}`，所以 `h` 越大 `AB` 越小，显然 `h\leqslant OC`，当且仅当 `OC\perp AB` 时取等。

isee

回复 2# kuing

估计楼主没有看到单位向量

kuing

这里向量只是个外壳包装，翻译过后就没用了，本质就是一道简单的几何题，而且还是初中范围内的。

isee

回复 4# kuing

把它搞到高中也行的。

isee

回复 5# isee

就利用主楼的图，由斯特瓦尔特（Stewart）定理$$(1/2)^2=\lambda\cdot 1^2+(1-\lambda)\cdot 1^2-\lambda (1-\lambda)AB^2，$$
下略

kuing

题外话，第一个链接的题目和解答其实是可以把代码复制出来粘贴到这里来的，就不用截图了。

方法：右键查看源代码，往下拉一点，就会看到如下的：

题目部分直接复制即可，答案部分麻烦一点，需删除一些多余的 html 代码，如 <br /> 等。

PS、这代码显然写得不怎么样，再往下看了下，估计整个网的代码也基本上是这水平……
还带这样的：

走走看看

谢谢大师们！
直接复制代码就行，那就太好了。

走走看看

回复 7# kuing

下面的东西，每次看到都参不透，不知道题目要算的东西表示什么意义。
算是怪兽吗？

走走看看

回复 9# 走走看看

zybang.com/question/b3cd86cafa37f727fa5e8d4b0cd64d67.html

答案是3/2，但没有解题过程。这个解题过程，似乎有点不完美。

游客

回复 9# 走走看看


    直接画图,很显然3/2.      点P在直线AB上,求OP的最小值.

敬畏数学

美哉！图形。

kuing

回复 9# 走走看看

和1#的题一样，纯粹就是考你从向量表达式到几何图形的翻译而已，翻译完就变成了很简单的平几，没啥怪兽的，算是常规题。

走走看看

谢谢各位方家。仔细看，也确实不像怪兽。

这里有两道向量题，相互矛盾，有可能就是怪。
$如图，在扇形OAB中，∠AOB=60°，C为弧AB上的一个动点，若\vv {OC}=x\vv {OA}+y\vv {OB}，求x+3y的取值范围。$

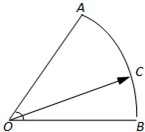
此题答案是[1，3]。
zybang.com/question/6cf97df85832cdab38189235aec7783c.html

$如图，在扇形OAB中，∠AOB=60°，C为弧AB上且与A、B不重合的一个动点，\vv {OC}=x\vv {OA}+y\vv {OB}，若x+λy（λ＞0）存在最大值，求λ的取值范围。$
mofangge.com/html/qDetail/02/g0/201310/6ee8g002328478.html
koolearn.com/shiti/st-2-526060.html

这道题的解答中写法存在一点问题，现改写如下：
$设射线OB上存在一点B'，使\vv {OB'}=\frac{1}{λ}\vv {OB},AB'交OC于C'。即B'也可以在OB线段外，此时与射线OC交点C'位于弧外。$
$由于\vv {OC}=x\vv {OA}+y\vv {OB}=x\vv {OA}+λy\vv {OB'}，再设\vv {OC}=t\vv {OC'}，则$
$t\vv{OC'}=x\vv {OA}+λy\vv {OB'}。$
$由于C'、A、B'三点共线，所以 t=x+λy。$
$又t=\frac{\vv{OC}}{\vv{OC'}}存在最大值，$
$故在弧AB（不包括端点）上存在与AB'平行的切线，$
$所以 λ∈(\frac{1}{2},2)。$

我的困惑是：
1、如何理解最后三句话？
2、这两道题是否矛盾？3不在下面这题的范围内。
请大师们指点！

isee

本论坛一堆这样的题解法全且优良，慢慢消化。

实在想不通，上坐标系+设角(点用三角表示)

走走看看

回复 15# isee

刚才看到了用坐标系的解法，比较好。
zybang.com/question/fe147f063c8402f23fbc99dec4cd7317.html
记得本论坛以前有人用参数法，利用坐标运算，再求导。
没有人用几何法呀。

kuing

回复 14# 走走看看

forum.php?mod=redirect&goto=findpost& … id=358&pid=23618 一年了还在纠结那个答案啊……

走走看看

回复 17# kuing


    是的呀，都怪我愚钝。这一次我又看到了这道题，所以，决心把这个几何法的解法搞清楚。

游客

写个代数的，练习下代码：
若$x^2+xy+y^2=1,x>0,y>0,$则$3(x+λy)^2+[(2λ-1)x+(λ-2)y]^2=4λ^2-4λ+4.$
x+λy有最大值，则$(λ-2)(2λ-1)<0$.

游客

在图形上，其实就是仿射坐标下的直线方程：
直线AE的方程为x+λy=1,要使x+λy有最大值，就是要使与AE平行的切线与狐的切点在狐上，
即当OP⊥AE于P时，要求点P在线段AE内，则点E只能在线段MN内。